The circle is really a special type of ellipse. In analytic geometry, an ellipse is a mathematical equation that, when graphed, resembles an egg. An ellipse has two focal points. The distance apart between the two points is one way of describing a particular ellipse. If the two points come together the ellipses become a circle with the point at its center.
The equation for an ellipse is,
x2/a2 + y2/b2 = 1
In this equation, “a” and “b” are constants that determine the shape of the ellipse, whereas x and y are variables, i.e., they can take on a host of values. When the value for x is known, the value for y is determined. Or, if it is y that is known, then x is determined.
If a = b, the equation becomes the equation of a circle of radius r,
x2 + y2 = r2
Let’s graph two equations–one an ellipse–one a circle.
Analytic Geometry – Graphing the Ellipse
For the ellipse, we are given an example that doesn’t look quite right! However, our instructor informs us that it is, indeed, correct.
4x2 + 9y2 = 36
Let’s change it and see why our instructor is correct. Since the number on the far right is not 1, but 36, let’s try dividing through by 36 to make it 1. Then,
(4x2 + 9y2)/36 = 1
This becomes
x2/9 + y2/4 = 1
Since 9 is the same as 3 x 3, and 4 is the same as 2 x 2, the form of this equation can be changed to,
x2/32 + y2/22 = 1
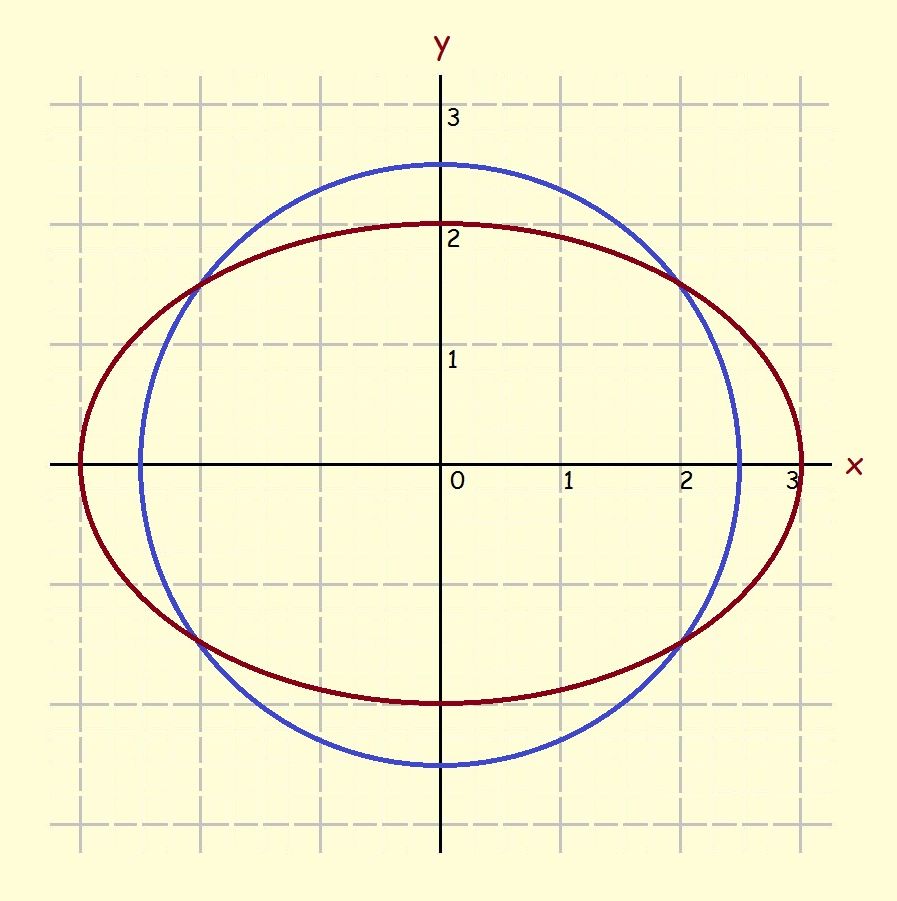
We now recognize it as an ellipse with a = 3 (or minus 3) and b = 2 (or minus 2).
We can graph the ellipse by calculating a collection of points as demonstrated in our earlier lessons, but there is an easier way to accomplish the task because we chose this form for our equation of an ellipse.
Interestingly, “2a” is the length of the ellipse (from x = -3 to +3), whereas “2b” is its height (from y = -2 to +2). How convenient and what an incentive to choosing this form for our equation!
Analytic Geometry – Graphing the Circle
Our instructor tells us to graph the circle,
x2 + y2 = 6.25
This converts simply to,
x2 + y2 = (2.5) 2
Since a circle is merely a special example of an ellipse, we gather—correctly—that we don’t need to figure points in this instance, either. It is simply a circle centered at the origin, or point (0, 0), with a height and a width of 2.5, both.
Note: You might also enjoy Algebra for Beginners: Student Perspective
← Back to Math-Logic-Design
← Home
