 What is a parabola, and of what use is it?
What is a parabola, and of what use is it?
If a sheet of paper is likened to an infinite plane in space, the x- and y-axes, drawn at right angles to each other, provide a means of describing each point on the plane of the paper in terms of an x and a y value. Thus the point (1, 3) tells us that beginning at the origin or center where the x-axis crosses the y-axis, if we travel one unit to the right and then three units up, we will have reached the point we seek.
Introducing the Parabola
Now we will pass on to describing a parabola.1 The parabola is an important mathematical “curve,” inasmuch as it describes, mathematically, the behavior of a number of important actions, such as the stretching of a spring. If the distance a spring is stretched is equal to the x-value, and the necessary force to accomplish this stretching is the y-value, the curve is a parabola. The force needed to stretch the spring greatly increases the further we stretch it. In the same way, the y values quickly increase even though values of x don’t increase much.
As the equation for a line is
y = mx + b
where m is the slope of the line and b is its intercept, so the equation for a parabola centered on the y-axis is,
y = ax2 + bx + c
where a ≠ 0
If a = 0, the term ax2 becomes zero, and the equation reduces to y = c, a simple line equation.
In the case that a = 1, b = 0, and c = 0, we have a particularly simple parabola. y = x2. For that equation, we can draw up a list of points to help us draw the graph. For instance,
(x, y)
(-3, 9)
(-1.5, 2.25)
(-1, 1)
(-0.5, 0.25)
(0, 0)
(0.5, 0.25)
(1, 1)
(1.5, 2.25)
(3, 9)
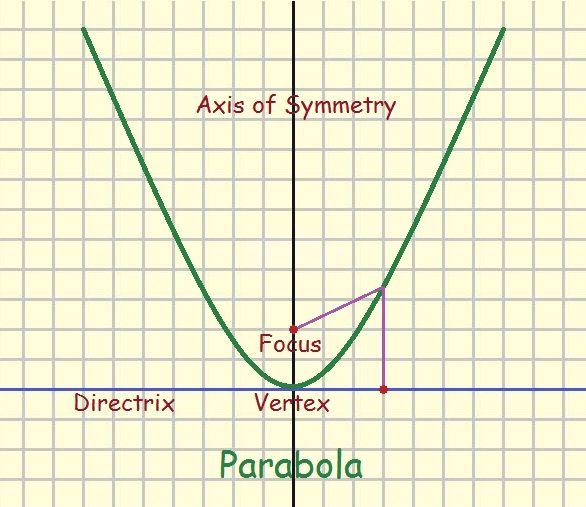
As is seen in the illustration, the parabola is shaped somewhat like the letter U, only with the branches of the U always getting slightly further apart. The bottom of the U intercepts the y-axis at b, even as was the case with the line. Since in this instance, b = 0, the bottom of the parabola is located at y = 0.
Practical Use of the Parabolic Shape
We’ve already seen how a parabolic curve describes the action of stretching a spring; however, there are many other practical applications utilizing the shape of a parabola. Parabolic mirrors are used in some telescopes and other optical devices. In addition, ideally the best shape to receive a signal is the parabolic dish.
Note: You might also enjoy Analytic Geometry: The Hyperbola
References:
← Back to Math-Logic-Design
← Home
