Determining the Equation for a Line from Two Points

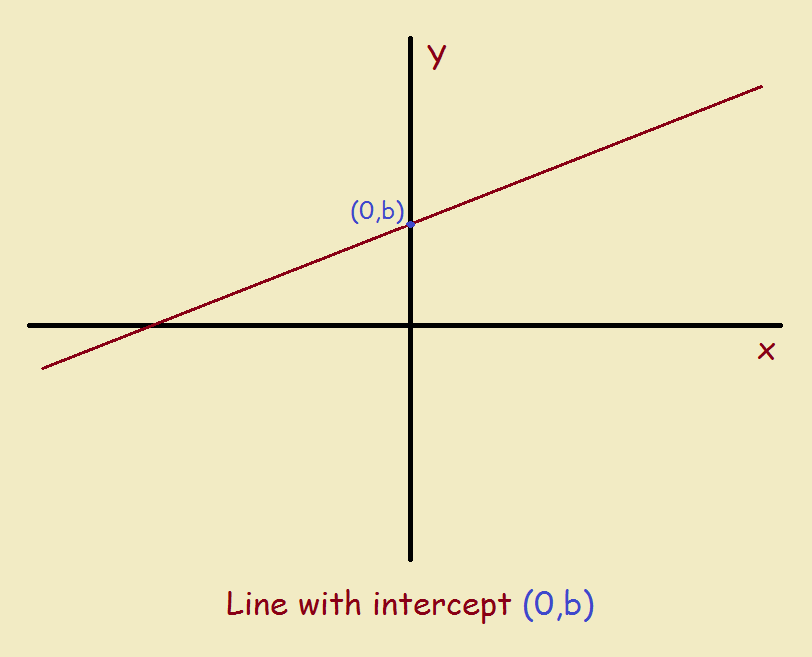
Lines can be drawn in three dimensions, but most analytical geometry courses stick to lines in two dimensions, generally using the Cartesian or XY coordinate system. The generic equation for a line may follow the form:

y = mx + b

where m is the slope (measure of tilt or steep-ness) of the line, while b is its intercept or intersection with the y-axis.

Equation for a Line from Two Points

A line can be determined and an equation derived from two points. In the Cartesian system, for instance, take two points, (2 , 3) and (– 1 , 5). The first number in each pair represents the x-value of a point and the second number in each pair represents the y-value.

Writing these points into the general equation y = mx + b, we have for Point 1,

3 = m (2) + b

For point 2, we have,

5 = m (– 1) + b

Solving the two-equation system for both in terms of b, we get, b = 3 – 2 m and b = 5 + m So 3 – 2 m = 5 + m and so, 3 m = – 2 and so,

m = – 2/3

Picking either of the two points and putting in this m value into the generic equation, 3 = – 2/3 (2) + b or, b = 9/3 + 4/3 = 13/3

b = 13/3

The equation for the line derived from the two points of our example is, therefore

y = – 2/3 x + 13/3

Verification of this equation is achieved by inserting the values of the second point into the equation,

Verification?

5 = – 2/3 (– 1) + 13/3 (Yes!)

Note: You might also enjoy Discrete Mathematics: What is a Point and What a Line?

← Back to Math-Logic-Design
← Home