
Of course, that is just plain nuts. Nevertheless, it raised the question, “Just how far away could a person see an object if nothing interfered? Let’s consider the answer to that question.
Conditions
First, we need to set conditions or ground rules.
Earth is sufficiently round to call it a sphere, so we treat it as such. In fact, we assume it is perfectly smooth even to an ant. Further, we assume the atmosphere is perfectly clear, and the observer has perfect eyes.
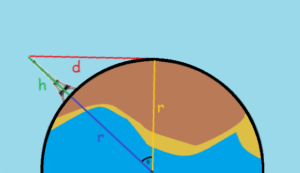
When we look out toward Earth’s horizon, we are actually looking along one of Earth’s tangents. If we look below the horizon, we see only the ground, not our object at maximum distance, d.
If we assume we have zero height, and we draw a line down through our body to the center of the earth, the second line is a radius, r, of Earth.
Finally, at the point of maximum distance we can see our object, we see only the very tip of the object. We draw a line through the object down to the center of Earth, a second Earth’s radius plus the height of the object, h.
The Math
Since we have described a triangle, and that triangle is a right triangle, we can employ the very simplest geometry and trigonometry. We write two equations…
r2 + d2 = (h + r)2
and
sin (θ) = d/(r + h)
where r is the radius of Earth, h is the height of the object, and d is the distance the observer can still see part of the object, despite Earth’s curvature making almost the whole of the object un-observable.
Rearranging the first equation, the maximum distance away on the earth an object can be (as the crow flies) and it can still be seen is,
d = √ h(h +2r)
Why bother with the angle and the trigonometry? It can be dismissed, but might interest the reader who likes to play mental games with himself.
For instance, if the object is of infinite height, the furthest distance it is still possible to see it is infinity! To a point… If the object is at an angle θ of 90° away from the observer, no matter what the height of the object, the observer can never see it.
The Eiffel Tower
The object of our choice, the Eiffel Tower, is 1,063′ tall. This converts to almost exactly 1/5 mile. Additionally, the median radius of Earth is 3,959 miles.
Substituting these values in our equation, we get,
d = √ 0.2(0.2 +7918)
Thus,
d = 39.8 miles
Not bad, really. And a reasonable figure, considering Earth is not flat but curves away from the observer. And as to the angle, we solve…
sin (θ) = 39.8 / (3959.2) = 0.01005
And therefore,
θ = 0.58 degrees
Note: You might also enjoy Was Mom Right? Is Eating Carrots Good for the Eyes?
← Back to Math-Logic-Design
← Home


I am lucky if I can see past the end of my nose. LOL Thanks for the lesson in Trigonometry. I think you can apply it to playing a game of billiards based on the angle of incidence = the angle of reflection. I was once told back in high school days.