Regular polygons are closed curves with a set number of sides and interior angles, each of identical value. How can one calculate the interior angles of polygons?
An equilateral triangle has three equal sides and three equal interior angles. Each angle is 60° or π/3 radians, adding up to 180° or π radians total.
A square has four equal sides and four equal interior angles. Each interior angle is 90° or π/2 radians, adding up to 360° or 2π radians total.
Interior Angles of Polygons
A short chart of additional polygons with their interior angles provides the following data:
- Pentagon 5 interior angles of 108° (540° or 3π radians total)
- Hexagon 6 interior angles of 120° (720° or 4π radians total)
- Heptagon 7 interior angles of about 128.57° (900° or 5π radians total)
- Octagon 8 interior angles of 135° (1080° or 6π radians total)
Clearly, an n-sided polygon has a total interior angle measure of
ф = (n-2)•π radians or ф = (n-2)•180°.
But how do we know, without resorting to a formula, that a triangle possesses an interior angle total of 180° or π radians? And how can we use this example to establish at least one other polygon’s angular total?
Determining Interior Angles Total of a Triangle
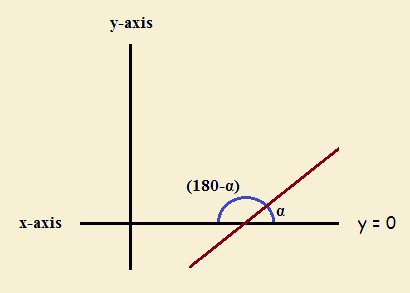
We begin with drawing a Cartesian Coordinate system with two variables, x and y. We will choose the x-axis (y = 0) as the simplest line for our discussion. The y-axis is perpendicular to it. So the angles between the x-axis and the y-axis for the four quadrants are (by definition) each 90° or π/2 radians. Above y = 0, the angles add up to 180° or π radians. Below that line, the same is true.
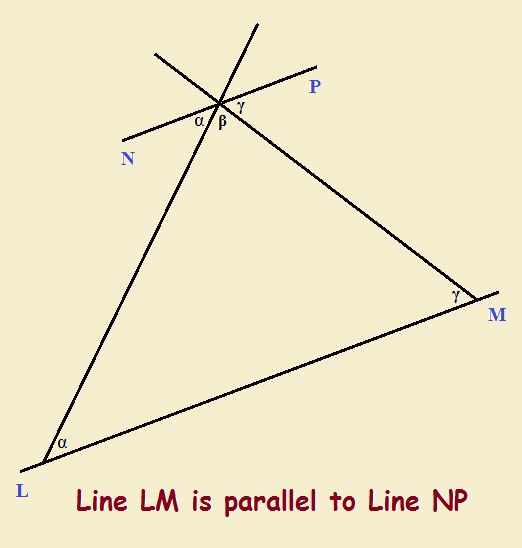
Now draw a line that cuts across the x-axis at any angle. The figure demonstrates this. The two angles at the intersection above that axis add up to 180° or π radians. So if there are three angles total, say α and β and γ , then α + β + γ = 180°. That being said, note our second image.
But If All Is Not Clear
But if all of this still leaves you a bit in the dark, see the video below. And even if it doesn’t leave you in the dark, but you wish to more deeply impress the material in your mind… see the Khan Academy video below.
Consider the Hexagon
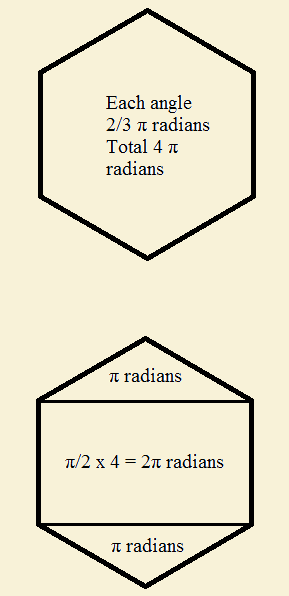
Now let us consider a regular hexagon. The hexagon possesses six identical sides, six identical interior angles. According to the formula for the interior angles of a regular polygon, we should arrive at the result of 4π radians. But we don’t have to draw them that way. We can, in fact, take a short cut and arrive at the same answer. Consider our figure featuring the regular hexagon…
Note: You might also enjoy Is a Circle a Polygon or Not? Implications for Calculus
← Back to Math-Logic-Design
← Home
