
We all know how to add, subtract, multiply and divide ordinary numbers, even if basic units are attached to them such as gallons, apples, feet, tons, and so forth.
4+3 = 7
5 lbs x 3.2 = 16 lbs
These two examples illustrate pure numbers in the first instance, and simple quantities in the second instance.
Introducing Vectors: What About Direction?
What if we toss in direction? Imagine a huge square, 5 miles on a side. We have to travel along the perimeter to travel from Point A to Point B, and then on to our destination, Point C (see the image). We thus travel 10 miles to reach Point C. If we could travel “as the crow flies”, we would only have had to travel a little over 7 miles.
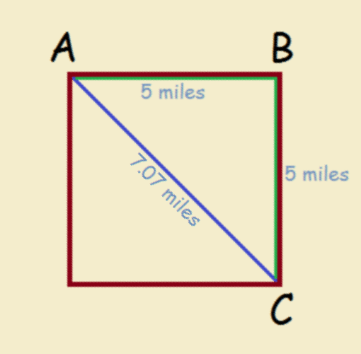
Let’s consider this example closely. Curiously, we had to drive 10 miles to reach our destination, which was actually just 7.07 miles away. Sometimes not only quantity, but also direction matters. We drove east, then south. If we could have driven southeast, we’d have used less gas!
Defining a Vector
We can speak of what we’ve discussed by introducing vectors. Just what is a vector? it is a mathematical entity that incorporates, not just the quantity (or magnitude), but also the “direction” in which that quantity is “aimed”. Vectors are important in mathematics, yes, but more importantly in physics and related scientific disciplines.
If you push a car, you have to push it in the direction you wish it to go. Now pushing is applied force. So forces are vector quantities. Gravity is a force. Jump off a building and you know where will you end up. Would you shoot a bullet without aiming the gun?
Indicating Vector Magnitude
We refer to speed by a number and units. A car may travel at 50 mph. Speed is not a vector. However, the term velocity, used in its strictest mathematical sense, incorporates the direction. We may use a small arrow above the variable “v” to remind us we are speaking of a vector.
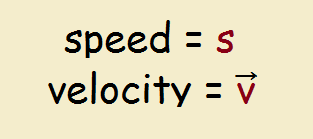
Introducing Vectors: Reconsidering Figure 1
Let us redraw figure 1, as vectors.
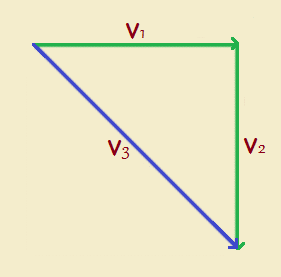
If we view the first leg of travel as not just miles traveled, but miles traveled East, we have vector 1, V₁. Our travel South is V₂. The total trip is V₃. That is,
V₁ + V₂ = V₃
We’ve performed a vector addition! For our example, we simplified matters by picking a vector addition involving a square. Obviously life is not always that simple. Consider our next example of vector addition. In this case, the vectors are not equal in magnitude, as is shown by their unequal length.
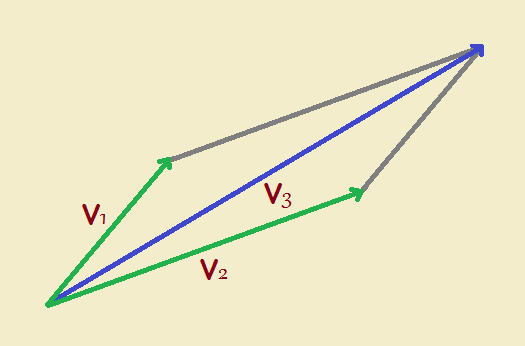
Notice that the other two construction lines (drawn in gray) are parallel to the two vectors. This helps us more clearly see that we are actually performing an addition. To verify that in your mind, check out Figure 5! Notice how it is essentially the same as Figure 4, with one exception.
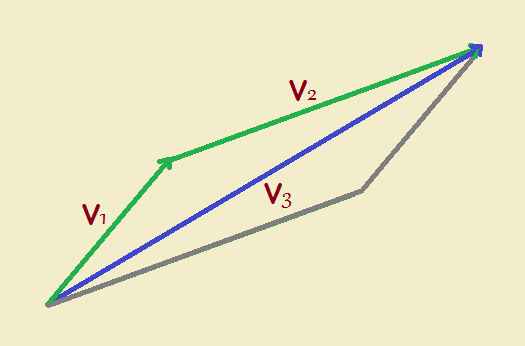
Clearly, vectors are added using equations based on trigonometric functions. And as the word trigonometric suggests, trigonometry is based essentially on triangles. We’ll derive and discuss those equations in a follow-up article.
First, though, and for “extra-credit” I highly recommend this video. It is excellent in its content and captivating in its presentation.
Note: You might also enjoy Sample High School Math Problems with Answers
← Back to Math-Logic-Design
← Home

That was a very clear explanation for vectors. Thank you.