 What are cylindrical coordinates?
What are cylindrical coordinates?
A coordinate system is a system that provides a way to describe points and other features of geometric figures in Euclidean space. Generally the best coordinate system is that system which adequately does the job in simplest fashion.
In this article, we will use (r, Φ, z) for our new coordinate system. Many use this, but others use a different assortment of letters, unfortunately. Forewarned is forearmed.
Cylindrical Coordinates – Introspection
When we’re working in two dimension, we are able to draw our coordinate axes using the sheet of the paper, representing a plane. Two orthogonal axes are drawn, one horizontal the other vertical.
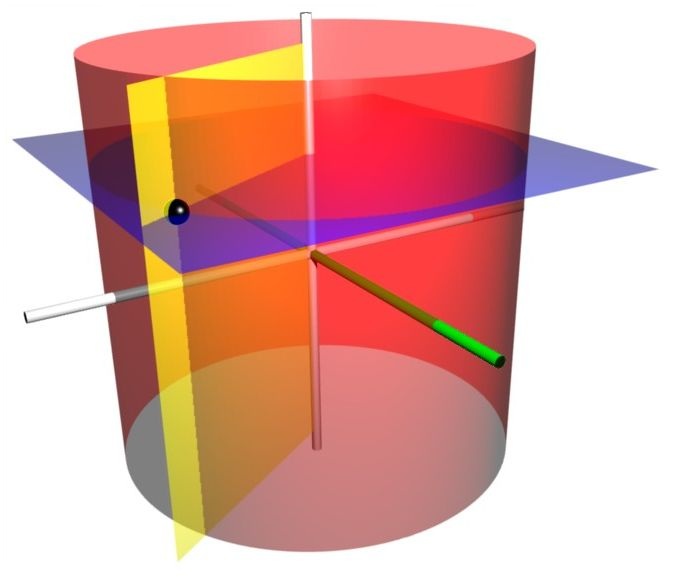
When using r and Φ the way we view the axes is really different from how we view them when they represent x and y. The r has no particular direction assigned to it, since direction totally depends upon the angle, and the angle has no association with any axis; however, we measure the angle from the x-axis on the positive side and increasing counter-clockwise.
Adding a Dimension
Now lay that paper with r and Φ on a table. If you’ve done that, we will add a vertical axis through the origin representing “z.” We will develop points with coordinates (r, Φ, z). Voila! There are now 3 dimensions. We now have 3-D space!
Equations written for 2-space change when applied to 3-space. For instance, the equation for a circle in polar coordinates of radius 2 is
r = 2
In 3-space, this is the equation represents, not for a circle, and not even a sphere, but a cylinder! Why? Because we have not specified z, z can be any value. In effect, we are constructing an infinite number of circles on top of and below each other.
Clarification by Illustration
If you can’t visualize that, recall that when you go to the supermarket and order a pound of sliced bologna, you get quite a few circular slices of bologna. What was the shape of the bologna before it was sliced? It was cylindrical, wasn’t it? It is the same with this equation, except the bologna is standing up and there are an infinite number of infinitely thin slices of “bologna.” How simple and yet elegant!
A New Example
Consider the equation,
r = z
What does this simple equation graph as?
Recall that in the x-y coordinate system the equation y = mx + b is that of a straight line. For y = x, the graph the straight line that passes through the origin (b = 0) and has a slope (m) of 1. Now since we did not designate any limitation to the values of the angle Φ, we can take this tilted line and produce a curve from it by rotating it (not changing the tilt). The resulting curve is a cone. See the image associated with this article.
Unfortunately, it is difficult to draw points in 3-space on a sheet of paper. For that reason in particular, I cite an online cylindrical coordinates graphing applet, below (Note: a number of browsers make it very difficult to impossible to run this applet).
Note: You might also enjoy Introduction to Polar Coordinates
References:
- Wolfram MathWorld: Cylindrical Coordinates
- Paul’s Online Math Notes: Cylindrical Coordinates
- Jacksonville State University: Cylindrical Coordinates’ 3-D Graphing Applet
← Back to Math-Logic-Design
← Home
