Equation for a Cone: The Mathematical Equation of Simplest Design

24Jul 2015 by Vincent Summers No Comments

equation for a cone You go to the mall and request a double scoop of Rocky Road ice cream. The fellow serving says “Yes,” and then he asks you asks if you would like that on a wafer or a sugar cone?

Since most have eaten ice cream since childhood (unless we are dairy or otherwise intolerant), the majority of people think of a simple v-shape hollow structure as a cone. It has a top. It has a bottom. But is this the kind of geometrical shape that mathematicians think of when they refer to deriving the mathematical equation of a cone?

A Mathematics Cone

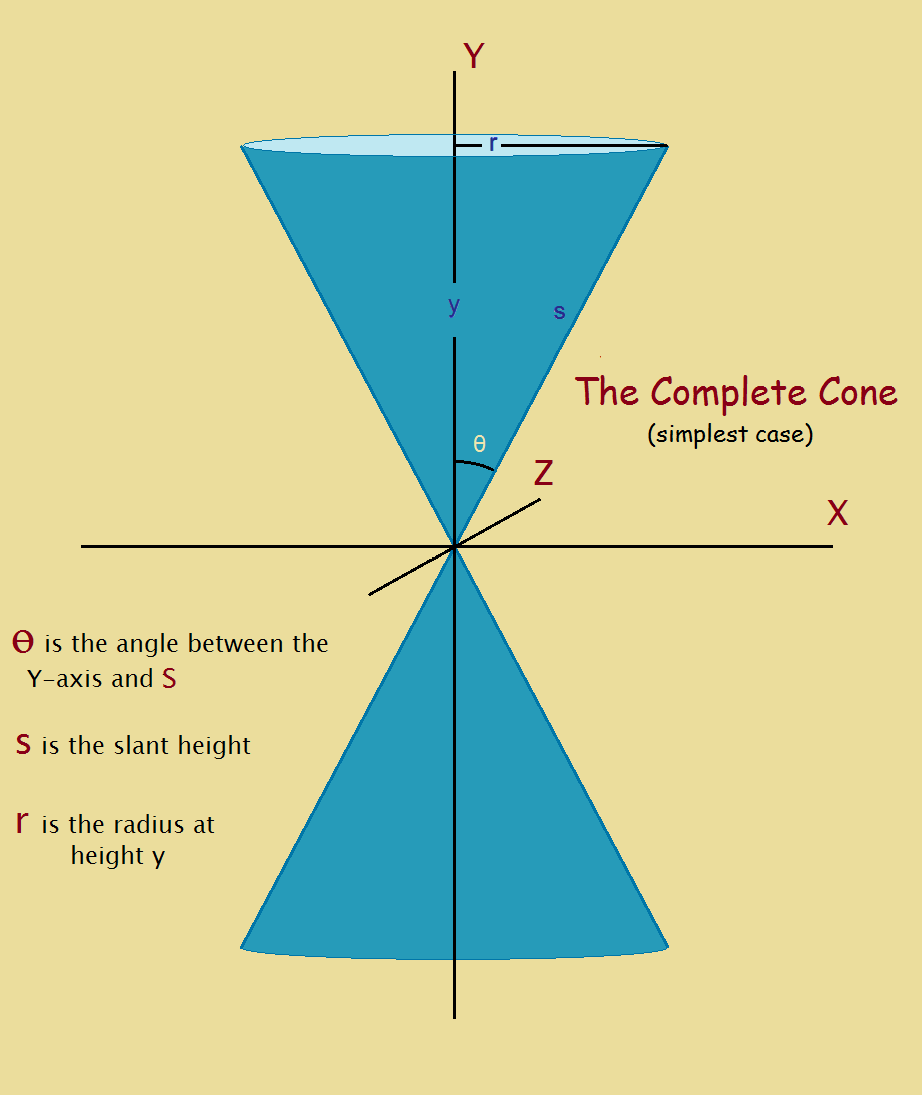
The cone of the mathematician bears some resemblance to that, but there are differences. The figure included with this article demonstrates that there are two v-shaped portions, not one. Both of those portions reach to infinity. If your high school mathematics instructor asked you to derive the mathematical equation for a cone, could you do it?

Impossible, you say? It’s too difficult? Actually, unless you are trying to derive the generic equation that covers all cases, it can be simple. In fact, I did it in high school, and I had no instructor urging me on. Undoubtedly the simplest case is that of a cone that aligns with an axis – say the y-axis – with the narrowest point aligning with the origin. That is the example we here choose.

Procedure

First, draw the x, y-coordinate axes, then draw the cone, as shown in the featured image. Put in a radius r, angle θ, height y, and slant height, s. Recalling basic geometry, such as the equation for a 2 dimensional circle, we see,

x²/a² + z²/b² = r² [formula for a circle]
and
r = y tan θ [by definition].

Therefore, by combination,

x²/a² + z²/b² = y² tan² θ.

For the simplest case, a = b = 1 [and keeping in mind the angle and tangent are constant], giving,

x² + z² = ky².