
You are to undergo testing. You look at your test paper and see many examination questions…
Many useful equations are arrived at by solving differential equations—for instance, the equation for the acceleration experienced by a falling object. This kind of activity involves some mathematical expertise and lots of care.
When I was working in industry, my partner told me that he suspected that there was an error in arriving at the navigation equations from its differential equations. He asked me to monitor his work as he solved the equations anew.
Mathematicians Do It Too
I know that when a mathematician (yes, even a good one) does math, he makes mistakes. I truly believe that he tends to get the easy stuff wrong (oh, it’s just arithmetic – breeze over this) and the hard stuff correct (obscure mathematics – concentrate). So the monitor’s purpose is to say, for instance, “No—3 times 5 is not 16”. Even—perhaps especially—mathematicians need an editor.
A Question Arises
So given the propensity for even a highly trained person to make errors, how do we compose mathematics examinations so that a student who seems to have mastered mathematical material does not perform up to expectation in an examination?
When I first met with students in college freshman mathematics, I found that their answers to examination questions consisted of various scattered computations and a number with the word, “ans” (meaning answer) circled to catch the professor’s eye. I call these “teacher friendly answers” (TFA) because grading takes minutes.
Another example of TFA is to make the question multiple choice, one example of which is the true/false question. With TFA there is no way for the teacher to see how answers to an examination questions are arrived at.
Recently a young friend, who was taking Calculus II at one of the United States’ leading universities, took the final. All of the questions were true/false questions. I was appalled. My friend said that the final grades were posted within hours. He missed the A he had expected by one point.
You’ve Got to Love It
Several years ago I had taught a course in mathematics at this university; all one hour tests and the final had some true/false and multiple choice questions. The professors were instructed to ignore any work done to arrive at the true/false and multiple choice questions, but I did look at some of the work. I don’t remember the exact problem but the naïveté shown by the student can be illustrated by the “solution” to the following problem:
64/16 = 4/1 = 4
The answer is of course correct, but she had crossed out the sixes, an error that should have been schooled out of her years ago: of course the first “6” means “6 times 10” and the second “6” means “6 times 1”. What was she doing in Calculus II?
My Approach to Examination Questions
I never taught there again. The mathematics department didn’t like me and I didn’t like it. TFA is completely unacceptable. My first task with the students was to teach them how to write. I add here that they did not like this. Let me talk about an alternate way of evaluating students: Writing Across the Curriculum . Here is a very simple example…
Problem:
If I buy four pounds of apples at $1.00 per pound and two pounds of oranges at $1.50 per pound, how much do I spend?
Solution:
Total = 4 x $(1.00) + 2 x ($1.50) = $4.00 + $3.00 = 7.00
Note that the solution is a correct English sentence, but written in mathematical language. The solution is a record of the student’s thought processes. And if, say, 4 X ($1.00) = is recorded as $5.00, the student still had one half of the problem correct.
I call this type of solution the Essay Solution (ES). The table below shows what the instructor will learn when marking a tests consisting of ES with answers (with TFA) and solutions (ES):
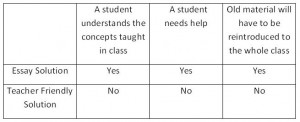
I remark here that it takes seconds to grade a TFA.
Writing Across the Curriculum is a little known effort where students are required to show all work in their homework and examinations, that is, write ES, as I illustrated above. One of my students was given a problem where he was told to use “m” to find another value, “m’”, to solve the problem, but he forgot how. So wrote he wrote nothing concerning the problem and got a grade of “0”. I told him that since his ES was, in fact, a letter to the teacher, he should write in his solution,
“I can’t remember the formula, so suppose the value I need is “m’.” He could then go on to solve the rest of the problem. This would exhibit some knowledge and a great deal of mathematical maturity.
Teachers of mathematics should be “correcting” tests, not just “marking” them with a “C” or an “X”.
-Ellen.
Note: You might also enjoy Requiescat In Pace (R.I.P. or Rest in Peace) – A Valid Phrase?
← Back to Math-Logic-Design
← Home
