
Symmetry About the Y-Axis
Symmetry about the y-axis means that if there is a curve that lies to the right of the y-axis, there is an identical copy of it to the left of the y-axis. That is, it is symmetrical if each x value can be replaced with –x. Thus, the parabola y = 1/2x2 is symmetric with regard to the y-axis. For every (x)(x) = x2 there is a (–x)(–x) = x2. Take note of the graph, below.
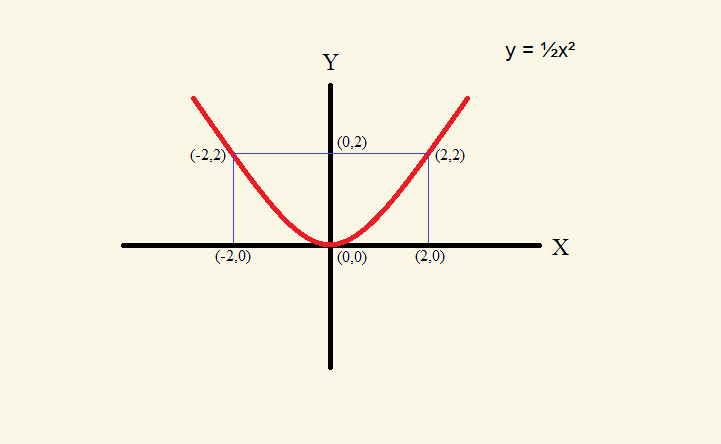
Note that for each and every point on the left side of the y-axis, there is a matching point on the right-hand side of the axis. And where there is no point on the left-hand side of the axis, there is no point on the right hand side, either. This is symmetry.
Symmetry About the X-Axis
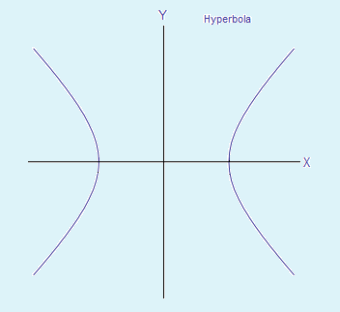
Next, consider the hyperbola x2 – y2 = 1. Superficially resembling two parabolas facing in opposite directions yet aligned along the x-axis, this curve is symmetric about the x-axis. Each y value can be replaced by –y. Here is a plot of that mathematical function. What is above the x-axis is a reflection of what lies below (Incidentally, this hyperbola is also symmetrical with respect to the y-axis).
XY Coordinate System Symmetry: The Origin
For the XY-coordinate system, the origin is, by definition, the point (0,0) where the x-axis crosses the y-axis. What function or curve is symmetrical about the origin? At first thought, it might seem a circle with its center at the origin would be the answer to that question. And in part, that is correct. But there are other functions and curves that are symmetrical about the origin. One example is the cubic parabola, y = x3. The condition of being symmetric about the origin, or symmetric with respect to the origin, exists if a graph is unchanged when reflected across both the x- and the y-axes.
First, examine the plot of the cubic parabola described above.
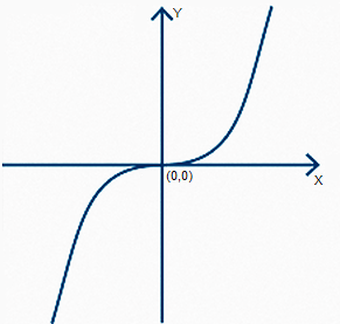
Next we flip the graph about the x-axis.
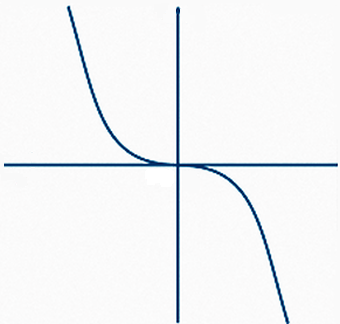
Then we flip the graph about the y-axis.
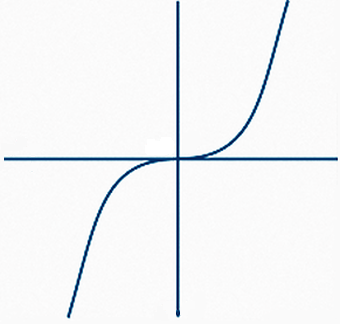
Overlap this end result with the original cubic parabola. The two are identical. The cubic parabola is, indeed, symmetric about the origin.
XY Coordinate System Symmetry: The Line Y = X
The line y = x is an easy one to draw. It intersects the origin and bisects the upper right and the lower left quadrants of the coordinate system. What example can be given of a curve that is symmetric about the line y = x?
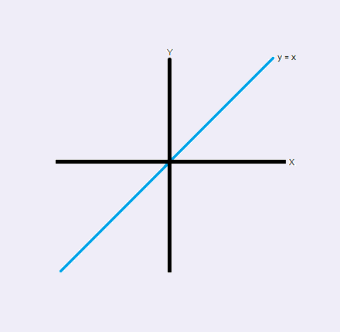
A mathematical equation is symmetrical to the line y = x if its y and x values can be interchanged. A very simple equation exhibiting such symmetry is that of another hyperbola, x times y equals some positive constant, c. We choose xy = 5.
A mathematical equation is symmetrical to the line y = x if its y and x values can be interchanged. A very simple equation exhibiting such symmetry is that of another hyperbola, x times y equals some positive constant, c. We choose xy = 5.
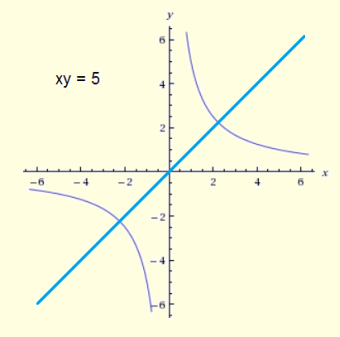
If the constant were negative, the resulting hyperbola would be symmetric, not to y = x, but to y = –x.
XY Coordinate System Symmetry: A Point
We choose the cubic parabola mentioned earlier, y = x3.
As it stands, it is symmetric about the origin, since applying a horizontal flip and then a vertical flip results in the very same curve we started with. But we are not looking for a curve that is symmetric to the origin, but some other point. There are two simple ways we can approach the matter.
- We could move the parabola by trying to devise an equation and center it at a particular point, (a,b)
- We could move the coordinate axes, leaving the parabola where it is, but in effect, changing its address.
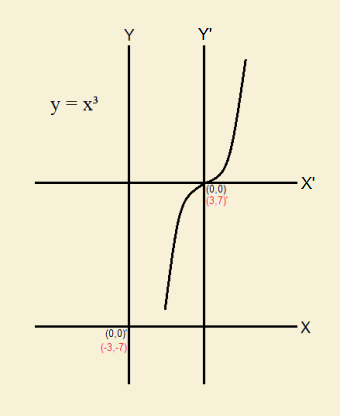
Let’s pick (3,7) for the point of symmetry. We graph the parabola with two sets of coordinate axes.
The initial set of axes, Y and X, matches the previous diagram and the original equation, yʹ = (xʹ)3. The new set of axes we call Yʹ and Xʹ. Notice that
xʹ = x + 3 and yʹ = y + 7
Substituting in the original equation, y = x3, we write
(y – 7) = (x – 3)3
So point (a,b), the point of symmetry for this equation is (3,7) using the translated coordinate system, our new coordinate system. And the equation itself is
(y – a) = (x – b)3.
References:
Note: You might also enjoy Simple Algebra II Graph Symmetries Discussion and Examples
← Back to Math-Logic-Design
← Home

That math is at my level, ok. The last bit was slightly above me but if I were to write it down, I think I would “get” it ok. As always, very clearly explained.
Thank you. The less that people feel my writing is “above them” the better I like it.