Is it possible to calculate the area under a curve with any degree of accuracy?
If we have a strong mathematical background, we may say, “Oh, that’s easy. It’s a matter of calculus.” But what if you didn’t take calculus? In fact, what if you never even attended high school?
Is it possible to achieve an answer? Is it possible to use reason to come up with the principles of calculus? The answer is, indeed it is. I met a man who did just that. He asked me how I would figure the area under a curve. But he did more. He wanted to show how me how he had succeeded in solving the matter himself on his job in construction work. I was so impressed I exclaimed, “You’ve just re-invented the Calculus!”
My Father the Eighth Grade Graduate
My father was a wonderful and intelligent (and special!) man. He only went to the 8th grade. In fact, I’ve wondered at times what he might have proved capable of if he’d had the chance to receive a thorough education.
What Dad Did
Big construction is big bucks. Dad needed to determine within close limits, how much raw materials he needed to build a structure with a curved surface. So he conceived an approximation process. He would draw rectangles within the curve and determine the total area of all of the rectangles. But he realized his choice of rectangle dimensions was important in determining the final result.
To Illustrate
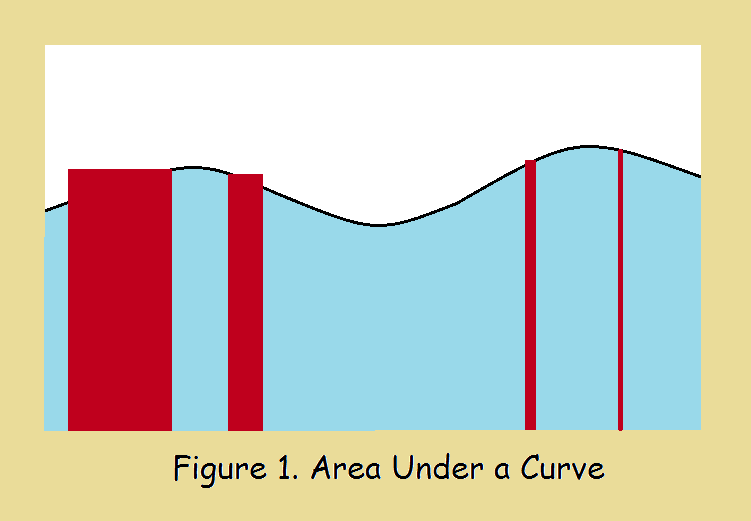
Take a close look at the image above. It features a wavy black curve. The area under this curve is what we seek to determine. How much area lies within the tan enclosure? Notice the assorted red rectangles. Note the widest one. Most of its area is part of the area under the curve. But it has a little too much area – the bit above the curve. If you divide up the area using rectangles of this size, your calculation result will be high when you are done.
Next, the second widest rectangle… Divide the whole area up into rectangles of that side, and again your results will be high. But not by as much as before. Now the next smaller rectangle. The result will still be off, but it will be better than for either of the two previous tries. In fact, you conclude as my dad did, the best choice of rectangle is the thinnest rectangle.
And, in the Limit…
Theoretically, if you increase the number of rectangles to an infinite number, you wind up with the EXACT area under that curve. You’ve just reproduced the underpinnings of the Calculus! Yes, that’s just what Dad did. Pretty smart for an eighth-grader, no? So never underestimate what you can do, giving up before you try. You just might surprise yourself, and those around you.
Note: You might also enjoy Mathematical Equation for a Cone
References:
← Back to Math-Logic-Design
← Home
I didn’t get as far as calculus at school but the way you have explained it and the way your father worked it out makes it seem like simple commonsense!
The older I get, Bill, the more I am of the opinion that all of us are essentially equally capable, or could have been, if outside impairments didn’t hinder the process. The simple is difficult and the difficult simple.
I didn’t do calculus either, but it wasn’t because I didn’t have the opportunity. I did, but I was not prepared to work at it! Nowadays I would love to have the opportunity, but have too much other work to do instead!
Sounds like me and the piano. I had opportunity to learn from a famous orchestral conductor, but chose to do what I could to discourage him, instead. HOW MUCH I regret that now.