Quasi-Spherical Orbits – by Author Bob Chester

The Most Interesting Curves You’ve Never Heard Of

by Robert G. Chester

Quick, what simple rotations simultaneously generate the circle, the parabola, and the intersection of a cylinder and a sphere? Can these rotations also subsume the hippopede of Eudoxus [1], the limaçon [2], Viviani’s curve [3], rhodonea [4], the lemniscate of Gerono [5], and Fuller’s “great circle railroad tracks of energy” [6]?

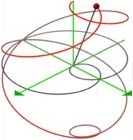
Quasi-Spherical Orbits, or QSOs, are the dynamic three-dimensional curves that result when a point rotates simultaneously about two or more axes. These intriguing curves provide insights and yield results in mathematics and physics alike.

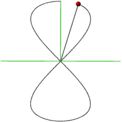
Viviani’s Curve

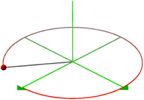
A point rotates in the right hand direction around the z-axis. The orbit is a circle in the xy-plane.

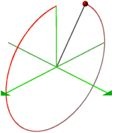
The point rotates in the right hand direction around the y-axis. The orbit is a circle in the xz-plane.

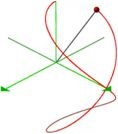
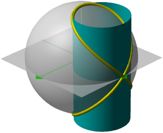
When a = b, and the point experiences both rotations simultaneously, the curve is QSO (1:1), or Viviani’s curve. Viviani’s curve is also the intersection of a sphere and a cylinder.

Circle, Parabola, Lemniscate of Gerono

The movement of the point can be described by the parametric equation

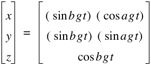
where a = b, g = 2πn, and n: 0 … 1 [7]. Setting the individual coordinates of equation 1.0 to zero yields well known curves on the orthogonal planes. Setting the x-coordinate to zero yields a parabola in the yz-plane.

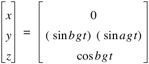
Setting the y-coordinate to zero yields the Lemniscate of Gerono in the xz-plane [8].

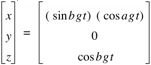
Setting the z-coordinate to zero yields a circle in the xy-plane.

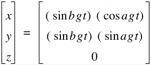
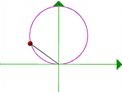
The model accents the importance of considering more than a single point-of-view [9]. Zeroing the x-axis creates a reciprocating half-wave motion. Zeroing the y-axis creates a point that travels counterclockwise in the “northern” hemisphere and clockwise in the “southern,” while zeroing the z-axis creates motion that is consistently counterclockwise. There is a similar “argument between viewpoints” as to the angular sweep-out of the point in a single orbit, which may be assessed at anything from 180° to 360° to 720° [10].

The Hippopede of Eudoxus

In the fourth century B.C., Greek astronomers had a problem [11]. They had noticed that a handful of the astral lights that filled the night sky moved or wandered across the backdrop of fixed lights [12]. The accepted explanation was that the moving lights were carried on crystal spheres in perfect circles around the Earth. What troubled sky-gazers was the fact that sometimes the wanderers seemed to reverse their motion. From time to time the lights were distinctly seen to go backward in their heavenly meanderings, only to soon reverse themselves and again resume their customary movement [13]. In the heavens, where all things were perfect, this was clearly unacceptable. Eudoxus of Cnidus attempted to explain the motion of the wandering lights with an ingenious scheme involving dual crystal spheres. One sphere, he said, rotated on an axis which passed through the center of the Earth. A second sphere was identical to and concentric with the first, but the axis of the second sphere was determined by two points on the first sphere and rotated with it. If the spheres then rotate with equal but opposite angular velocities, a light on the second sphere will describe the figure eight in the sketch. Because it resembles a horse fetter, the curve is called the hippopede of Eudoxus [14].

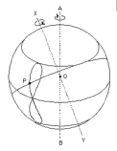
Equation 1.0 can be easily modified to produce the hippopede. The modifications needed are all scalar quantities. They have no effect on the nature of the curve. It is still created by simultaneous rotations on two axes.

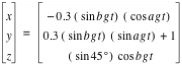
The Limaçon [16]

Twenty-one centuries after Eudoxus, a French lawyer and amateur mathematician, Etienne Pascal, studied curves with an inner loop [17]. In 1650 his contemporary, Gilles de Roberval, named them limaçon, which means “snail” in French [18]. It seems unlikely that either man realized their snails were related to Eudoxus’ work. The parametric equation for the limaçon is

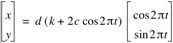
where c = k = 1, d = 0.5 and t: 0 … 1. This gives a curve in the xy-plane with a single inner loop.

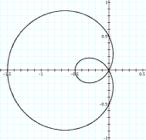
However, the projection of QSO (3:1) on the xy-plane is also the limaçon.

Rhodonea

Rhodonea were named by the Italian mathematician Guido Grandi because he thought they resembled roses [19, 20, 21]. Rhodonea have the polar equations

r = sin kθ
or
r = cos kθ

When k = 3, the curve is a trifolium.

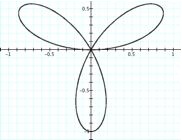
But the trifolium is also produced by the projection of QSO (1:3) on the xy-plane.

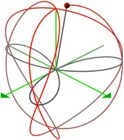
Fuller’s “Great Circle Railroad Tracks of Energy”

In 1975 and again in 1979 Buckminster Fuller discussed what he considered to be the basic energy exchange mechanism in the Universe [22, 23]. Energy, Fuller said, never travels in straight lines. It is stored on and shunted along the multiple “great circle railroad tracks of energy” of the tetrahedron, octahedron, icosahedron, and Vector Equilibrium, Fuller’s name for the cuboctahedron. When energy gets a green light to go from one of the great circles to the next, he said, it can do so by crossing over one of the inter-atomic-sphere bridges, or Grand Central Stations, where the great circles intersect. There is always the problem with Bucky’s model of how a charge manages to jump from one track to another. He did not explain how the jump was achieved. The QSO model shows how this can happen, and it’s not a jump. The model demonstrates that the charge is sequentially on all the great circles, or on the only one non-simultaneous great circle. Dipole QSO 2(1:2) demonstrates that one great circle can pass through all the vertices of a polyhedron. It shows how a single dipole may non-simultaneously constitute an entire system.

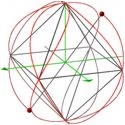
This short introduction to Quasi-Spherical Orbits has barely scratched the surface. It has shown how simultaneous rotations about two axes can generate the circle, the parabola, and the intersection of a cylinder and a sphere. It has shown that these rotations also subsume the hippopede of Eudoxus, the limaçon, Viviani’s curve, rhodonea, the lemniscate of Gerono, and Fuller’s “great circle railroad tracks of energy.” Do you suppose QSO rotations could also generate the cardioid, all epi- and hypotrochoids, and three-dimensional Lissajous figures as well as an infinite number of polygons, polyhedra, and all but one of the Platonic solids? And that’s only around two axes. Imagine the possibilities when there are more.

Note:

Need further help to envision these complex curves? If so, here are some QSO instructional videos for your enjoyment and enlightenment.

Footnotes:

[1] Eudoxus of Cnidus, 408-355 B.C.

[2] Etienne Pascal, 1588-1651

[3] Vincenzo Viviani, 1622 -1703

[4] Guido Grandi, 1671-1742

[5] Camille Christophe Gerono, 1799-1891

[6] Buckminster Fuller, 1895-1983

[7] For the derivation of this equation, see QSO — The Mathematics and Physics of Quasi-Spherical Orbits, chapter. 2, by the author.

[8] Camille Christophe Gerono, 1799-1891

[9] This description is adapted from Quasi Spherical Orbits — Particles On Great-Circle Tracks Develop Significant Forms

When A Second Spin Axis Is Introduced, © Michael Burke, 1992. Private correspondence with the author, 1992 Jun 13.

[10] Zeroing the x-axis yields 180° x 2 = 360°

Zeroing the y-axis yields 90° x 2 = 180°

Zeroing the z-axis yields 360° x 2 = 720°

[11] This section is adapted from the introduction to QSO — The Mathematics and Physics of Quasi-Spherical Orbits, by the author.

[12] English: planet from Greek planasthai, to wander.

[13] The “backward motion” of the wandering lights refers to the retrograde motion of the planets.

[14] Greek hippos, horse + Latin impedire, to entangle, fetter.

[15] J.J. O’Connor and E. F. Robetson, Eudoxus of Cnidus

[16] Latin: limax, snail

[17] Etienne Pascal, 1588-1651

[18] Gilles de Roberval, 1602-1675

[19] Guido Grandi, 1671-1742

[20] rhodo- from Greek rhodon, rose.

[21] E. Weisstein, “Rose.” From MathWorld–A Wolfram Web Resource.

[22] Buckminster Fuller, 1895-1983

[23] Fuller, 1975, p. 187; 1979, p. 455

References:

• Chester, R. G., QSO — The Mathematics and Physics of Quasi-Spherical Orbits. Intellectual Property Associates, Tumwater, WA, 2009.
• Fuller, R. B., Synergetics. Macmillan, New York, 1975.
• Fuller, R. B., Synergetics 2. Macmillan, New York, 1979.
• Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica. Second edition. CRC Press, Boca Raton, 1998.

Copyright retained by author. Published with author’s permission on 2-22-2016.

Download the Author’s Publication, free of charge, in PDF format: http://vixra.org/pdf/1803.0263v1.pdf

← Home