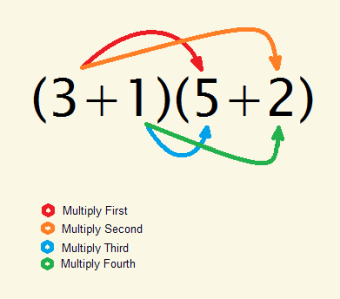The Algebra Distributive Property – A Simple Introduction

The algebra distributive property lets you multiply a sum by multiplying each part separately and then adding those amounts together. These words are bound to confuse the reader, so let’s consider an example that will demonstrate what we mean.

The Example

We want to multiply 4×7. Let’s write it as (4)(7). Then,

(4)(7) = 28

Now let’s replace 4 with its equivalent, 3+1. And let’s replace 7 with its equivalent, 5+2. Then,

(3+1)(5+2) = 28

This seems to be a pretty strange way to write 4×7, doesn’t it? Yet in mathematics – in algebra-style notation – it is just as correct as 4×7. In this form, we can hopefully explain in an understandable way, how the algebra distributive property works.

Refer to the diagram to see how we can do each multiplication and addition in a way that is consistent and can help us to avoid confusion and mistakes.

(3)(5)+(3)(2)+(1)(5)+(1)(2) = (15) + (6) + (5) + (2) = 28

Notice (perhaps surprisingly to the beginner) we arrive at the correct answer.

Generic Format of the Algebra Distributive Property

A simple format for the algebra distributive property if it involves only four simple unknowns is,

(a+b)(c+d) = ac + ad + bc + bd [Answer]

Our Final Problem

Now, using what we’ve just learned, let’s try a new problem. We will combine constants and/or variables to make each of our unknowns. Let’s try,

(3x²+4y)(5x+2)

Using the order of multiplication we’ve illustrated above, we get

(3x2+4y)(5x+2) = 3x²•5x + 3x²•2 + 4y•5x + 4y•2

or,

(3x²+4y)(5x+2) = 15x³ + 6x² + 20yx + 8y [Answer]

Do these really match? For confirmation, let’s pick a value for x and for y, say x = –1 and y =2. Then,

(3x²+4y)(5x+2) = (3(1)+4(2))(5(–1)+2) = –33

and

15x³ + 6x² + 20yx + 8y = –15 + 6 –40 +16 = –33

The results match, as well they should!

Note: You might also enjoy Mathematical Powers – A Simple Insight

References:

• Math is Fun: Distributive Law

← Back to Math-Logic-Design
← Home