Mathematical Powers – a Simple Insight

Multiplication is one of the simpler operations we perform on numbers. As kids we had to learn the multiplication tables, one times two equals two, two times two equals three, three times two equals six, and so forth. It didn’t take long before most of us were comfortable multiplying simple numbers. But sometimes we multiply the same number times itself. In that case, we can write out the multiplication in the usual way, or we can write it in terms of mathematical powers.

Mathematical Powers – a Simple Illustration

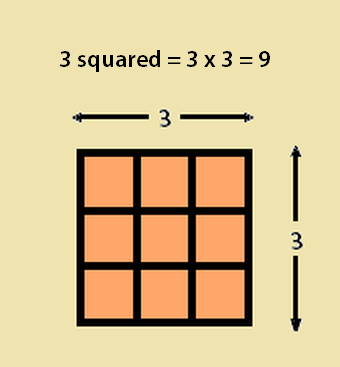
Let’s consider the example of three times three. That can be written either 3 x 3 = 9, or in powers notation,

3² = 9

This tells us three to the second power (or three squared) equals nine. Consider the two images associated with this article. One is a square with sides equal to 3. The other is a cube with its three sides each equal to 3 as well. The former square contains within it nine 1 x 1 inch smaller squares. The cube contains within it twenty-seven 1 x 1 x 1 smaller cubes.

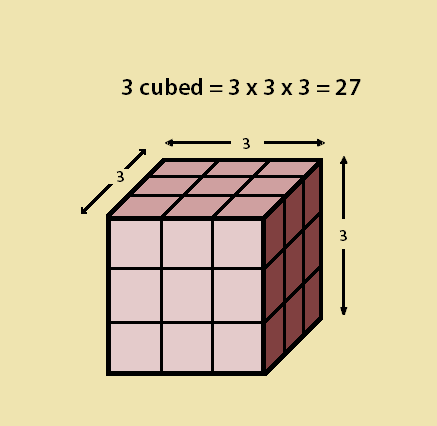
I know of no one who can draw a geometrical figure that demonstrates the mathematical powers expression 3⁴ = 3 x 3 x 3 x 3 = 81. But we should need no such figure. The simple insight we’ve provided using the square and the cube should suffice.

One Last Thought

For one last help, one last aid, consider this. 3² = 3 x 3. And 3 = 3 x 3 x 3. In the first case, the power 2 also represents the number of 3’s that are multiplied together. In the second case, the power 3 represents a similar thing. So the multiplication power expression 3⁸ consists of eight 3’s multiplied times each other, or

3⁸ = 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 = 6561

Note: You might also enjoy Factorials? What are They? A Simple Kind of Mathematics Shorthand

References:

• West Texas A&M University: Exponents

← Back to Math-Logic-Design
← Home