Are Imaginary Numbers Real? Yes, they are! Everyday numbers such as we use when calculating taxes for the year are called real numbers. Examples are 1003, 5/8, or -27.2. Other numbers, however, often in the world of the microscopic, are called “complex numbers.”
Complex Numbers
Complex numbers are numbers that contain both a “real” and an “imaginary” part. Any complex number, “n,” can be written in the form, n = a + bi. In this equation, “a” is a real number—as is “b.” The “i” or imaginary part stands for the square root of negative one. Why is this number referred to as imaginary? Consider.
Imaginary Numbers
The square root of four is two, because 2—squared—is (2) x (2) = 4. Note that negative two is also a square root of four, since (-2) x (-2) = 4. Similarly, the square root of nine is three; it is also negative three.
Using these examples, is it possible to write a value for the square root of minus one? If you can figure out how to do that, mathematicians will be forever indebted to you! Even (-1) x (-1) = 1, not -1. Because mathematicians don’t know how to assign a number to the square root of minus one, does this mean it does not exist and is unreal? No. In fact it is of great importance in scientific applications such as particle physics.
Consider the historically famous mathematical equation (see image) named after the famous 18th century mathematician, Leonhard Euler. The letter “e” is not a variable, as one might at first suppose, but it is an irrational number constant. The word irrational means it cannot be written in fraction form, but has numbers beyond the decimal point that stretch on an infinite number of places. It may be written, 2.71828…
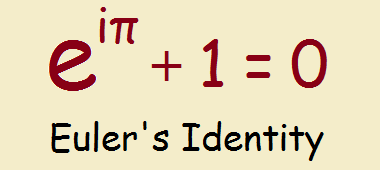
Would you like to watch a video that presents convincing evidence of the usefulness of imaginary numbers?
Note: You might also enjoy What is a Negative Number?

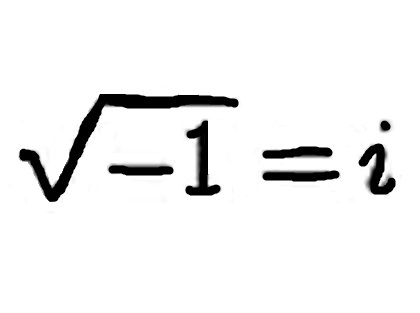
You have “e” wrong in your paragraph on Euler’s identity. 2.718281828459
Thanks. The two digits were, as you suggest, reversed. I’d like to say it was dyslexia, but I have to mark it up as old age…