
You walk into a bar and order a beer. The guy next to you engages you in conversation and gets very friendly. Then he suggests you play a little game just for fun. It will cost you just X dollars to play, and if you win he will give a sum greater than X. Here are some examples of bad bar bets.
Bar Bets: The Königsberg Bridges Game
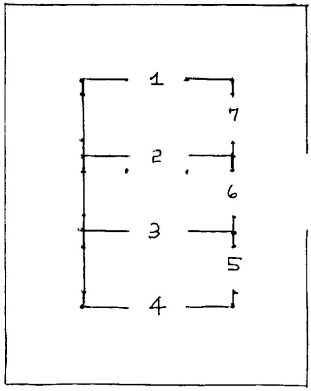
A student of mine brought me the floor plan shown in Diagram I and said, “A man in a bar said if I paid him five dollars and was able to trace through each of the doors labeled 1 to 7 exactly one time he would pay me twenty five dollars. I tried several times, but did not succeed. Will you show me how to do it?”
I looked at the plan. I knew immediately that it was a reconfiguration of the classic Königsberg Bridges Problem illustrated in Diagram II: walk through the German town and cross each bridge exactly once. Study Diagrams I and II and convince yourself that they present the same problem. It was proven to be incapable of solution by the famous mathematician, Euler (see my article on the Euler Bank).
When I tried to tell the student about this impossibility, he could not comprehend what I was saying. “But if you try harder, you will probably get the solution,” he said. He finally believed me. This is certainly a bad bet.
Diagram II
These investigations by Euler (bless him) brought into being a new branch of mathematics called graph theory.
Bar Bets: The Birthday Game
There are at least 24 customers in addition to the proposer of the game and the player. The player pays the proposer $25 to play the game. Each of the non-playing customers announces his birthday. The player bets that no two customers have the same birthday. If he wins he gets $50.
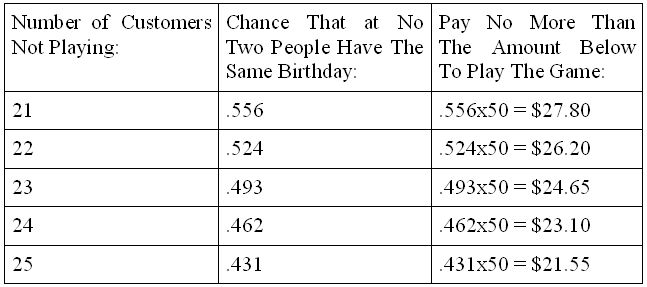
But Diagram III shows that the game is unfair to the player. With 23 people in the room, the chance of the player winning is .493 or about 1/2. After that the chance that the player will win steadily decreases as the number of customers increases. At 256 and above the chance is zero; the proposer always wins if there are 256 or more people in the room.
If there are 21 customers in the bar and you played the game 100 time, the number of times could expect to win is about 100x.556 = 55.6 or, rounding, 56 times. You would have won 56x$50.00 = $2,800 But it would have cost you 100x$25 = $2,500 to play. You should pay no more to play the game than is shown in the third column.
Bar Bets: The Hat Check Game
There are at least two customers in a bar in addition to the proposer and the player. The player pays the proposer $10 and each of the non-playing customers writes his name on a piece of paper, folds it and places it in a container. The papers are then thoroughly mixed, and each customer picks and keeps one of the papers at random. The player bets that no one picks his own name, and if he wins he gets $50.
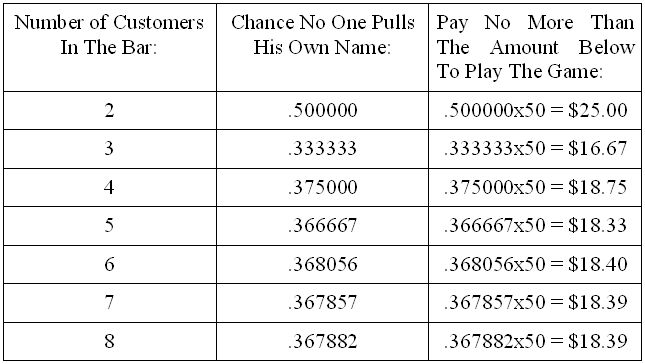
But diagram IV shows that the game is unfair to the player. If there are 6 customers in the bar and you played the game 100 times, the number of times you would expect to win is about 100x.368056 = 36.8056 or, rounding, 36 times. You would have won 36x$50.00 = $1,800.00. But it would have cost you $5000.00. You should pay no more to play the game than is shown in the third column.
The game is called the Hat Check Game because it is traditionally given as follows: if a number of customers at a restaurant check their hats and the hats are given back at random, what are the chances that no one gets his own hat back? Curiously, as the number of participants increases, the values in column two settle down to .367879… = 1/e, where “e” is the famous number named after Euler (bless him).
Here is a note about using statistics for winning games. If the chances are winning are, say, .2 = 2/10, if you play a large number of times, say, 1000 times, you will win about .2 x 1000 = 200 times. In a casino, the house has the advantage. If you hit a winning streak at the beginning, stop playing; in the long run, the house always wins.
–Ellen Hetland Fenwick.
Note: You might also enjoy Consider the Lilies
References:

Statistics like this are fascinating, especially when you see that the “con man” proposing the game possibly did not do well at school, yet can understand very well that they will make a profit on this.