Consider the lilies. The following problem once was posed to me:
Consider water lilies of a certain species. A group of them is planted in a pond, and each day the planting doubles in size. On day 28 after the initial planting, lilies completely cover the pond. When do lilies half-cover the pond?
The usual guesses are a) day 14 (half of 28) and b) day 27 (one day fewer than for complete coverage).
Solution a) is proven wrong by seeing that if the pond is half full on day 14 and the planting doubles on the 15th day, then the pond is completely covered by the 15th day.
Solution b) seems reasonable, but a bit of analysis shows that this solution may not be correct. For instance, if the initial planting covers any portion of the whole pond greater than 1/2, the pond is never half-covered; or if the initial covering was 1/3 of the pond.
What’s Wrong Here?
The problem with the problem is that there is incomplete information in the statement of the query, so let us reword it:
Problem: Consider the lilies of a certain species. A group of them is planted in a pond, and each day the planting miraculously doubles in size at midnight . Under what initial condition does there exist a day when the pond is half covered? How many days after planting is it half covered?
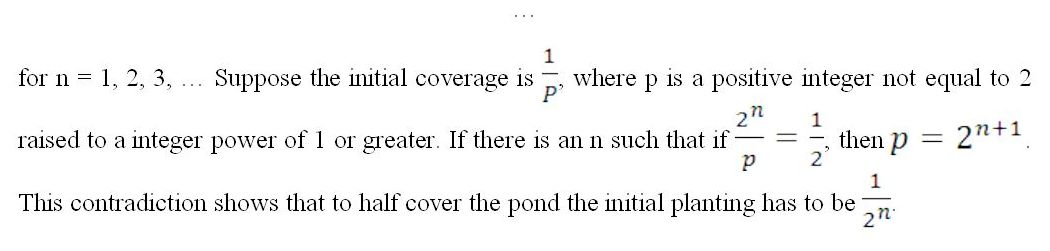To avoid that mathematics above, you could try the riddle on your friends worded the following way:
Consider water lilies of a certain species. A group of them is planted in a pond, and each day the planting doubles in size. On day 28 after the initial planting, lilies completely cover the pond. If there is a day so that the pond is half covered, what day is that?
Then there is a correct answer: the day is day 27.
Note: You might also enjoy Bar Bets to Avoid
References: