Draw two intersecting lines in space, illustrated below. The mathematician will not want to leave this simple drawing without completely pointing out its features and labeling those features. We do so to begin our understanding of basic (circular) trigonometric functions.
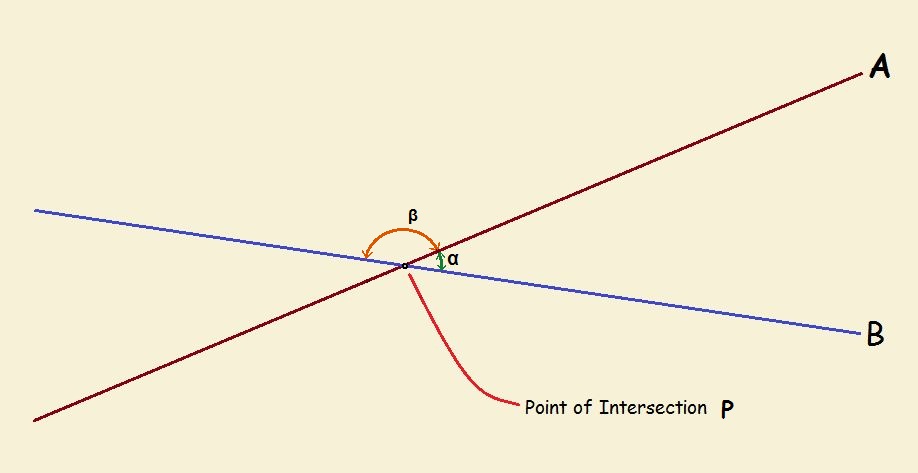
We label the point of intersection of course – P will do. But the intersection produces what looks like slices in a pie. The size of those slices of pie were determined by how the two lines intersected, how “wide apart” the lines are. We label these as angles α (alpha) and β (beta).
Superimposing a Circle
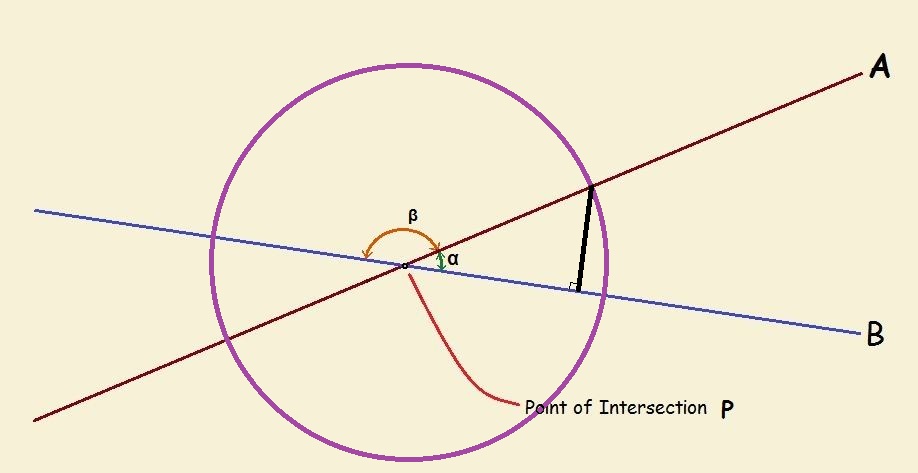
The title of this paper is understanding basic circular trigonometric functions. So at this stage, let us superimpose a circle onto the above figure. In addition, let us construct a perpendicular line segment from line B to the upper point on the circle where line A and the circle intersect.
Cartesian Coordinates
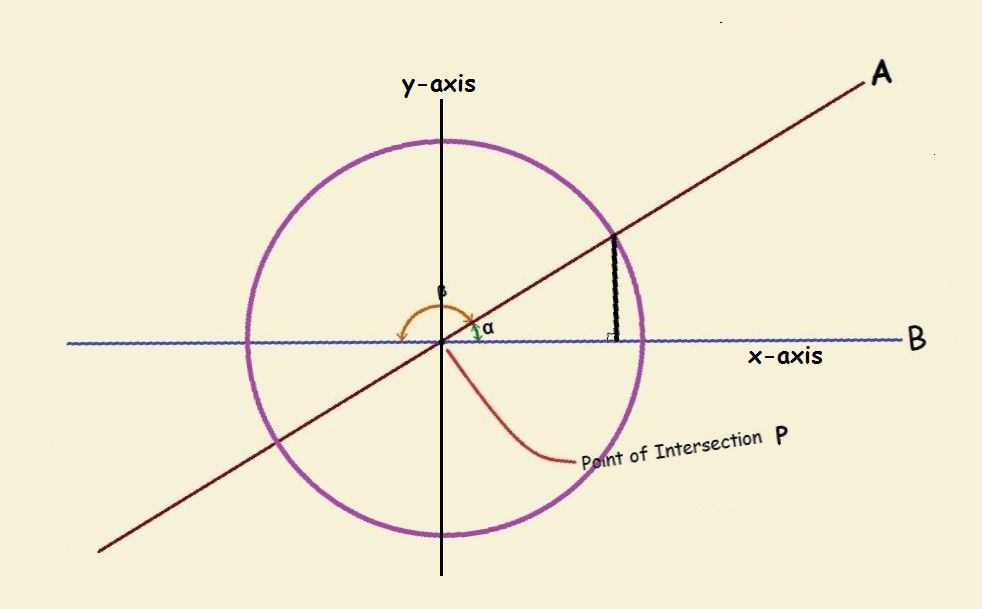
Now let us rotate the above figure until Line B is horizontal. It coincides with the x-axis. The perpendicular line between this axis and the point on the circle where it coincides with Line A thus becomes a y value. In doing all of this, if we pass another perpendicular line through point P and identify it as the y-axis, P becomes the origin.
Let’s remove excess baggage from the image. Let’s also label line segments that relate to our further discussion. We will call the longest leg of the triangle drawn, h, for hypotenuse. The line segment along the x-axis we’ll call x, and the line segment parallel to the y-axis we’ll call y.
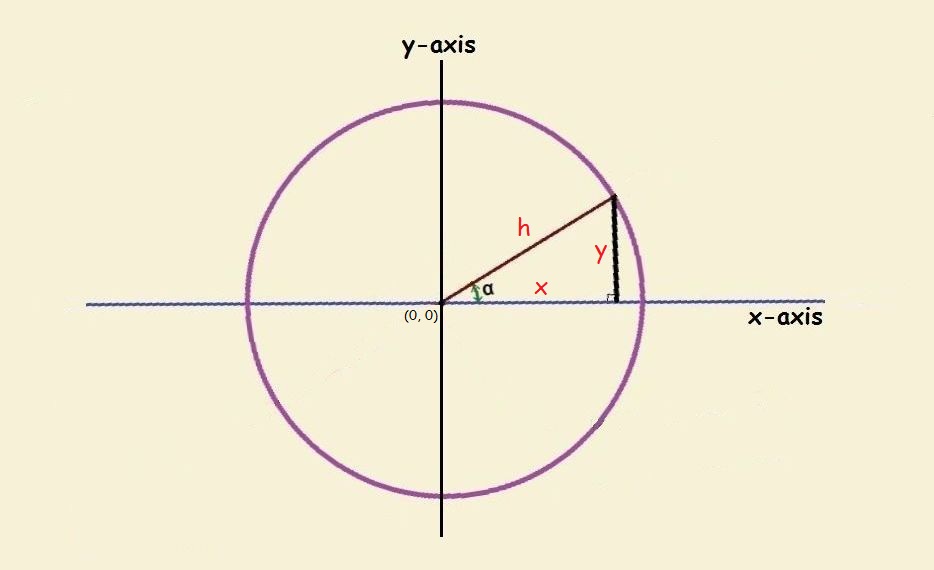
Simple Trigonometric Functions
Now we can capture the nature of an angle by means of ratios. For example, we know that as an angle increases in size, the side opposite the angle increases. We also know that if the circle encasing the triangle drawn in Figure 5 increases in radius, the side opposite the angle increases. However, by proportion, the radius, and, logically, the side labeled x increases.
So, let us define functions of the angle based on the side opposite the angle in terms of the side next to the angle (in our drawing, the x-value) and/or the hypotenuse of the triangle. We write:
- sine α = y/h
- cosine α = x/h
- tangent α = y/x
- cotangent α = x/y
- secant α = 1/cosine α = h/x
- cosecant α = 1/sine α = h/y
These functions are usually written in shorter form as
- sin α = y/h
- cos α = x/h
- tan α = y/x
- cot α = x/y
- sec α = 1/cos α = h/x
- csc α = 1/sin α = h/y
Each of the above functions (oddly enough) are of great importance in physics, especially in the physics of the atom!
As the value of the angle changes, so does the value of y and of x. These values are often charted to the fourth or fifth decimal place. And those values can be graphed. One very famous circular trigonometric function graph is that of the sine function.
Consider the Sine Wave
Notice the plot of the function y = sin (x) below. Notice how its value fluctuates smoothly in repetitive fashion. This result might have been anticipated by a close consideration of Figure 5, above. The sin is equivalent to the value of y over h. The upper right quadrant of the coordinate system is positive in x and positive in y. As one approaches the y-axis, the sin rises from 0 to 1.0000 as the angle reaches 90°. It then decreases, but remains positive until its value reaches 0 again at 180°. Greater than 180°, y becomes negative to an ever greater degree until it reaches 270°. Then, although the sin remains negative, it becomes ever less so until it reaches 0, at which time the process repeats itself. Graphing this, below, tells the story succinctly.
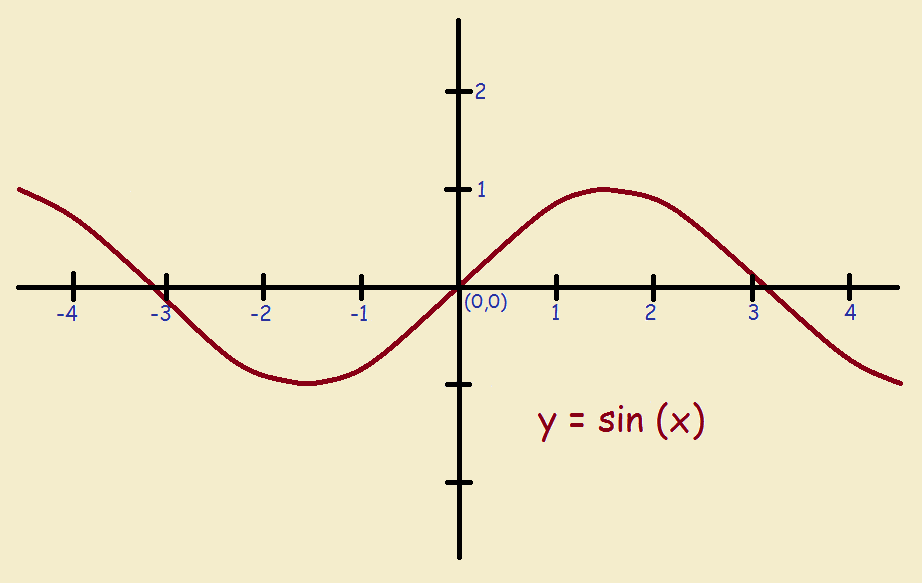Does this graph remind the reader of a wave, such as that of a photon of light traveling through space? Interestingly, as a wave increases in frequency of crests and valleys, so too does the energy of the light it describes. And the length between crests, defined as the wavelength of that light, varies inversely.
Trigonometric Functions: A Practical Example
Let’s consider one practical example that utilizes the sin function. Trees in the open generally grow straight and tall. It can be hard to determine their height. But you have a device that can tilt your view upwards in specific angular increments. You back off from the tree and look at its tip top. The distance between you and the tree is x. The angle is α. Then,
sin α = y/x
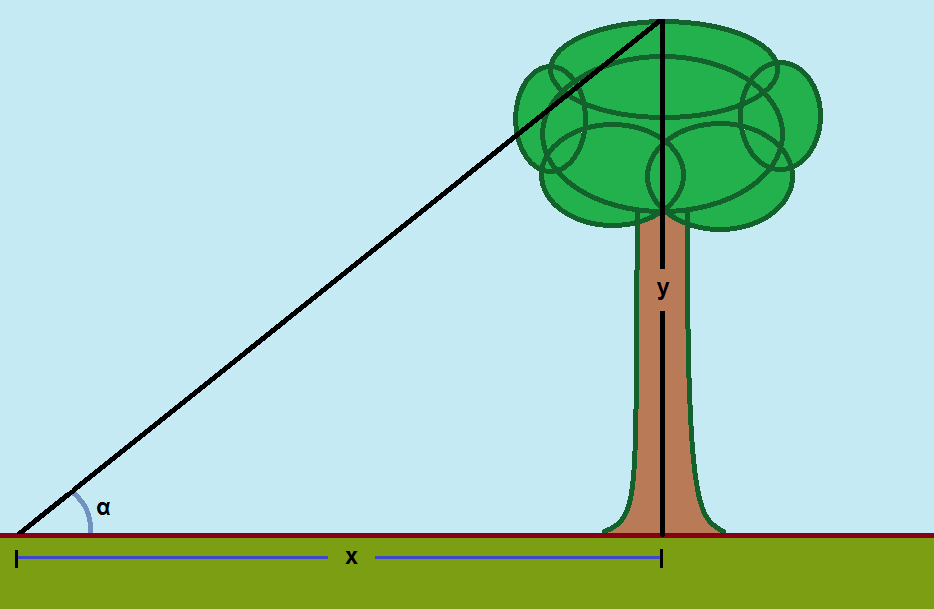
That is, the sin of the angle of view equals the height of the tree divided by its distance. You can look up the sin in a mathematics chart in the back of a trigonometry book you own, and so,
y = x · sin α
The height of the tree equals the distance you are away from the tree times that number. As an example, you stand away some 50 feet from the tree and gaze at its top, at an angle of 40°. A math book tells you the sin of 40° equals 0.6428.
y = 50 · 0.6428
The tree is just over 32 feet tall.
Note: You might also enjoy Simplifying Mathematics: Introducing Vectors and Vector Addition
← Back to Math-Logic-Design
← Home
