There’s no point attempting to explain the precise nature of gravity here. Most of us are aware it is Earth gravity that enables us to remain standing on the planet. Gravitational force operates on all matter.¹
Is Matter the Same as Weight?
No, the two are not the same. To illustrate, say a man is seated at the doctor’s office and he is invited back. He is requested to stand on a scale. It says he weighs 210 lbs. We write w = 210 lbs.
Now say that man is an astronaut. Ah! Next week he is deep in space. If he removes his restraints, he begins to float. He is weightless!² That is, w = 0 lbs. Yet his mass remains the same. That is, m ≠ 0. Weight is a variable, while mass is a constant.
The Representative Equation
The force of gravity between two objects, connects a gravitational constant, the mass of each object, and the distance between them. We write the equation
Fattractive = G·(m1m2) / d2
The gravitational force equals a constant characteristic of gravity (G) times the product of the masses of the two objects(m1m2) divided by the distance between them, squared (d2).
Worthy of Mention
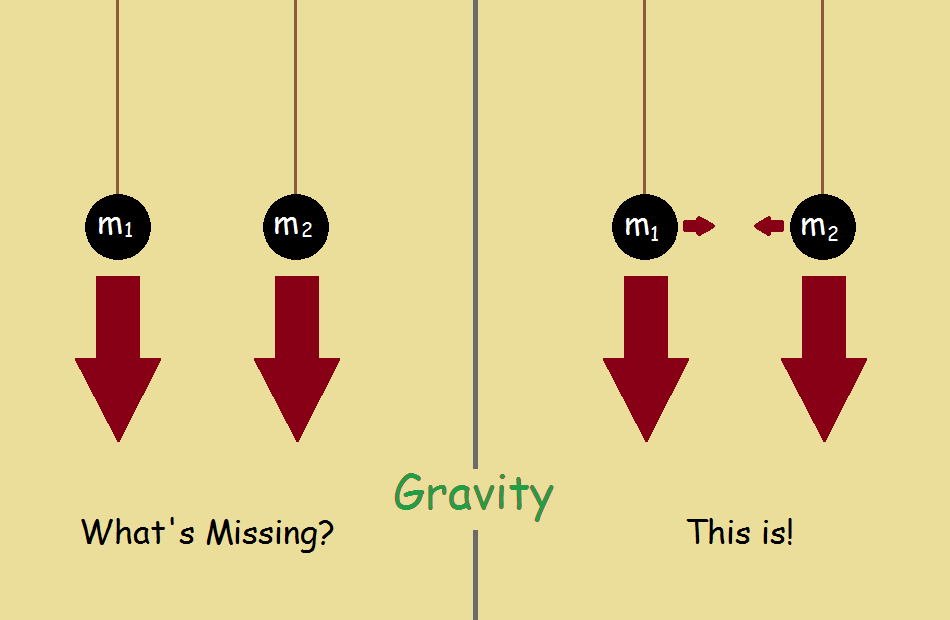
Since all bodies of matter come under its purview, not only to respond to gravitational force, but to generate it, an object within Earth’s gravitational grasp must answer, not to Earth gravity alone, but to every other mass object as well. Notice the provided illustration.
Let’s Plug In Some Numbers
It’s time for an example. We will employ for our example, the SI or International System of units. We begin with the value of the gravitational constant, G.
G = 6.674 x 10-8 cm3 / g·sec2
From this, it is obvious our units of mass must be grams. Time is in seconds. Distances in centimeters.
Let’s choose m1 = 10 lbs. Converting to grams, we have 4.54 kilograms. Now m2 = 20 lbs. In grams, we have 9.08 kilograms.
For a distance apart, we will choose 1 inch. This is 2.54 centimeters. This is 0.0254 meters. Squaring, we have 0.000645 m2.
What is the gravitational force between these two masses?
Calculations
The gravitational force between the two masses m1 and m2 is
Fm1, m2 = 6.674 x 10-8 · 4.54 kg · 9.08 kg / 6.45 x 10-4 m2 = 4.3 x 10-11 Newtons.
How does this compare with the gravitational force between Earth and, say, m2?
A Comparison
What is the mass of Earth, anyway? It is approximately 5.97 x 1024 kg. Our reaction between Earth and the 20 lb. (9.09 kg) weight is
FEarth, m2 = 6.674 x 10-8 · 5.97 x 1024 kg · 9.08 kg / 6.45 x 10-4 m2 = 5.61 x 1013 Newtons.
What’s the Difference?
Dividing the force involving Earth with the force involving the 10 lb. weight, we achieve a difference ratio of 1.30 x 1024 times. This means the strength of the interaction with the 10 lb. object versus the interaction with Earth is roughly
1 / 1,000,000,000,000,000,000,000,000 times, or 1 one-septillionth times as strong!
This is why we usually discount gravitational interactions of objects on Earth, one with the other, if the planet itself is not involved.
1 Forms of energy possessing mass experience the pull of gravity as well.
2 We ignore, for the moment, any interactions between the astronaut and his immediate surroundings.
Note: You might also enjoy How Far Can Perfect Eyes See? An Ideal Earthly Scenario
← Back to Classic Science
← Home
