It’s fun and very instructive to figure out the math equations for parallel and perpendicular lines.
The basic mathematical equation for a line is,
ax + by = c
Here are three examples of line equations:
- 2x + 3y = 6
- 4x – 2y = –5
- –x/3 + 2.47y = √3
Slope-Intercept Form
One of the most useful formats for the equation of a line is the slope-intercept form. That form is written,
y = mx + b
The variables here are x and y. The letters m and b are constants that represent the rise or tilt of the line (slope, m) and the point at which the line crosses the y-axis (intercept, b).
So the first of the three equations for a line listed above is written in the slope-intercept format as,
y = 2/3 x + 2
This tells us,
m = 2/3 and b = 2
Our desire now is to write equations for parallel and perpendicular lines based on the slope-intercept equation as cited above.
Deriving Equations for Parallel Lines
Two parallel lines have the same slope but a different intercept.
If the first line is written y = mx + b, then a parallel line may be written y = mx + b1.
Using our example line, y = 2/3 x + 2, all of the following are parallel lines:
- y = 2/3 x + 8
- y = 2/3 x – 7/16
- y = 2/3 x + √13
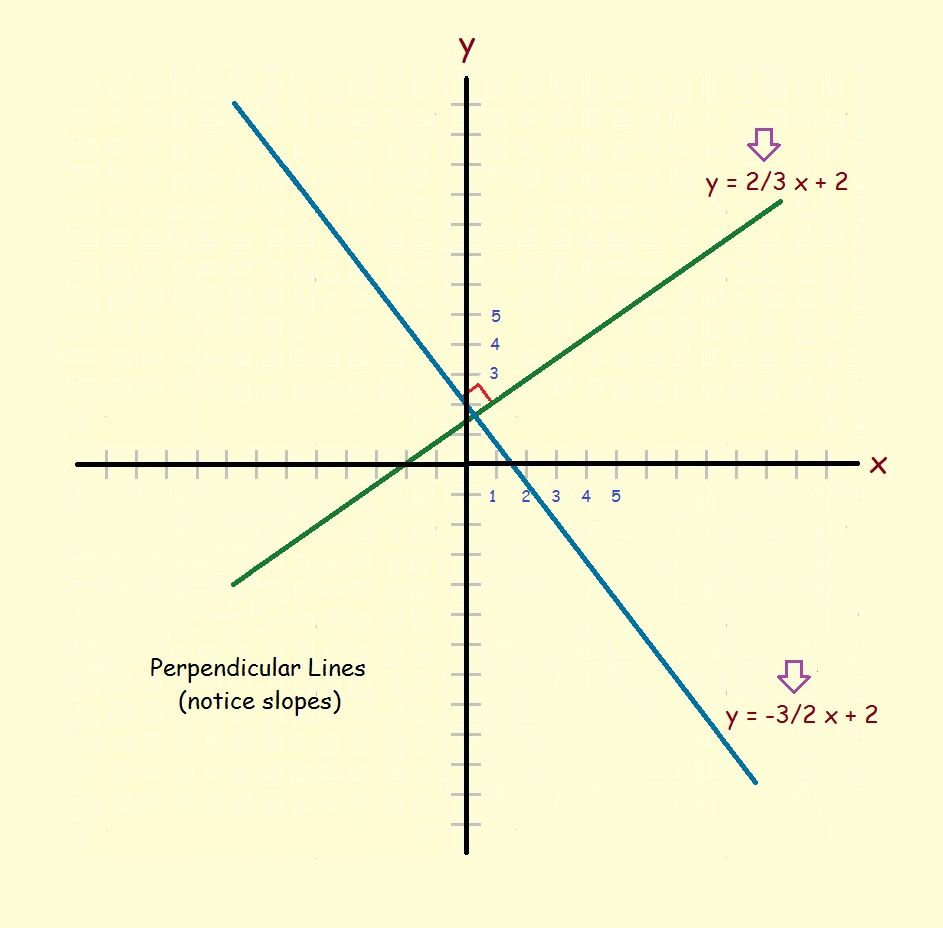
For Perpendicular Lines
There are two differences for perpendicular lines. At first, you might be inclined to think as I once did, that you just take the inverse of the slope. This sounds logical, but is wrong. If the slope of the line is positive, it rises as x increases. The inverse of that slope is also positive and rises as x increases. But a perpendicular of such a line must rise to the left rather than to the right.
For that reason, the sign of the slope must also change. This leads us to the correct conclusion that a line with 2/3 slope is perpendicular to a line with a slope of –3/2. That is,
y = –3/2 x + 2 [perpendicular line]
See the image.
There is an in-depth online proof of this located on the Central Oregon Community College website.
Note: You might also enjoy Point on a Line, a Line on a Plane, and a Plane in Space
← Back to Math-Logic-Design
← Home
