 Each point has a specific location. Two points determine a line. Three points determine a plane. Let us consider some simple math derivations to arrive at a format for each. For simplicity’s sake, we will use the familiar x, y, z Cartesian coordinate system. We begin with a point on a line.
Each point has a specific location. Two points determine a line. Three points determine a plane. Let us consider some simple math derivations to arrive at a format for each. For simplicity’s sake, we will use the familiar x, y, z Cartesian coordinate system. We begin with a point on a line.
First, Point on a Line
In space, a single point has an x value, a y value, and a z value. If the coordinate system chosen for the point is a simple 1-D line, then only one variable – say x – is needed to describe it. Then, since there is no y or z to consider, the mathematical description of the point is
x = c
But let us, for reasons that will be understood later, write it using two constants instead of one
Ax = C [Equation of a Point]

Second, Line in a Plane
We move on from the point on a line. Choosing the xy-plane, we will choose two distinct points (x1,y1) and (x2,y2).1 The slope of the line, m, is
m = (y2– y1) / (x2-x1)
Since a line is infinitely long, every line must either intersect the x or the y-axis, and most often, both. For derivation purpose, we can choose whichever axis is intersected as our y-axis. The intercept point we label (0,b). We choose that point to represent (x1,y1). This results in
m = (y2-b) / (x2-0)
Removing the subscript and multiplying through,
y = mx + b
Is there a superior general equation for a line? Yes.
Ax + By = C [Equation for a Line]
This equation appeals to the intellect. Consider: Move the expression in x and the constant, c, to the right-hand side of the equation. Divide both sides by b, and you get?
y = (-A/B)x + C/B
This is the same style format as the slope-intercept equation for a line. The -a/b is equivalent to the slope, m, while the far right term is equivalent to the intercept.
Now we have discussed only lines within the xy-plane. But the letters x and y were chosen at random. Any other letters, say v and w would do as well.
Third, Plane in Space
Extending the logic above, we now have the three points, (x1,y1,z1), (x2,y2,z2), and (x3,y3,z3). From these three points, three combinations of two points can be drawn from “the hat.” Through each of the pairs a single line can be drawn.2 However, it takes only two lines with two “slopes” to characterize a plane.
The general equation of a line in a plane was given above. Logically, and by extension, the equation for a plane in space is,
Ax + By +Cz = D [Equation of a Plane]
Consider the example graph for z = 2x + 4y, below.
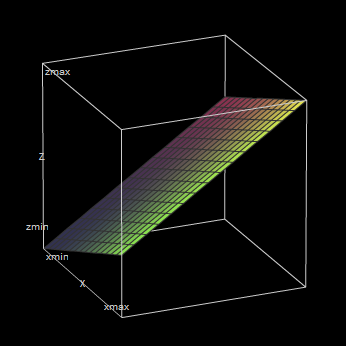
In Conclusion
What an interesting thing it is to compare the mathematical expressions next to each other, for a point in a line, a line in a plane, and a plane in a coordinate system.
- Ax = C [point]
- Ax + By = C [line]
- Ax + By + Cz = D [plane]
What comes after that? Whatever it is (let’s call it t) ought to be described by
Ax + By + Cz + Dt = E
1 Three distinct points for 3D (all 3 cannot satisfy the same y = mx + b equation).
2 Any pair of lines from the 3 points will intersect.
Thanks to mathematician Mike DeHaan for proofreading the material.
Note: You might also enjoy Mathematical Equation for a Cone
References:
- Ask Dr. Math: Equation of a Line in 3-D Space
- U. of Washington: Dept. of Mathematics: Basic Equations of Lines and Planes
← Back to Math-Logic-Design
← Home

I really need to improve my math. I was good at it when it was mainly arithmetic, but once it moved into algebra and geometry, it needed more work and I didn’t bother. 🙁 I got as far as the slope of the line but have never needed anything more than that. But I find math more interesting these days. – getting old! 🙂
You say you “have never needed anything more than that” but I would suggest that if you did, in fact, learn more math (“improve my math”) you would see opportunities to use it where you did not imagine it could be applied.