Do you have a basic knowledge of the spherical polar coordinate system?
A coordinate system provides a way to describe and plot math functions using two or three variables. If there are two variables the graph is 2D. If there are three variables, the graph is 3D.
The Cartesian Coordinate System
The most familiar coordinate system is the Cartesian coordinate system. Typical variable names are x and y in 2D (although variables can have any name), and x, y, and z in 3D. Every point of every 2D function has a unique value in (x, y). Every 3D function similarly has a unique value in (x, y, z).
The Polar Coordinate System
This 2D coordinate system uses one distance coordinate and one angular coordinate, typically r and theta (θ). A circle can be drawn in this coordinate system simply by making the distance coordinate a constant and the angle completely variable. Make the angle a constant and the distance completely variable, and you have an equation for a line. Each point of each 2D function has a value in (r, θ).
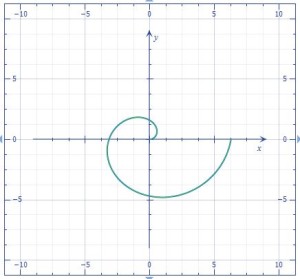
Although it is to be expected that a function can be graphed on any of a number of coordinate systems, it is interesting to derive conversion formulas. For instance, a circle can also be graphed in a strictly Cartesian coordinate system and the equation in that system can be converted to its corresponding equation in the polar coordinate system.
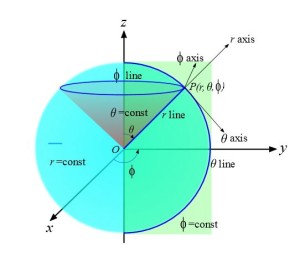
The Spherical Polar Coordinate System
The spherical polar coordinate system is like the polar coordinate system, except an additional angle variable is used, frequently labeled as phi (φ). A point in a 3D function graphed in this coordinate system is then assigned a value (r, θ, φ).
Angles can be given in degree units – a complete rotation amounting to 360° – or it can be given in radians.
360° = 2π radians.
If both angles are allowed to be of any real value whatsoever, whereas the value of r is constant, one obtains the equation of a sphere. For example, r = 8 is a sphere of radius 8 in the spherical polar coordinate system.
If one angle is held constant and one angle and the distance are variable, a cone results. If both angles are constant and the distance variable may assume any value, one again has the equation for a line.
Note: You might also enjoy Introduction to Cylindrical Coordinates
References:
← Back to Math-Logic-Design
← Home
