Geometry Stop the World – I Want to Get Off

Many of us had to take plane geometry in high school. If you remember it was, “Theorem, Proof, Theorem, Proof…” What kind of ammunition did you use for the proof of a theorem? The axioms and previously proven theorems. I know, I know. Some of you want to forget the anguish. But I want you to recall the fifth axiom…

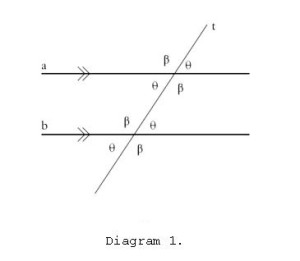
Plane Geometry – Diagram 1

Look at Diagram 1. directly below. Line a is parallel to line b. That is lines a and b don’t meet.

Axiom V: Through the point where line t meets line a there is no other line that can be drawn parallel to b.

Now it took about 2,000 years of struggle, but eventually mathematicians found that if you changed the fifth axiom slightly to no parallels you get a different geometry.

Diagram 2

Look at Diagram 2. Here is a model for the geometry: the surface of a sphere. The lines are great circles (I know, I know;  you want to call lines straight. But a line is just a collection of points!)

Axiom V: Look at the line through point A and B.

Point C is not on this line, and ALL lines through C meet the line through A and B.

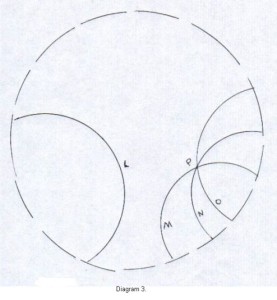
If we change Axiom V slightly to many parallels, you again get a new geometry. Look at Diagram 3. below. Point P is not on line L. Lines M, N, and O contain the point P, and all three lines and many others through P are parallel to L (Diagram 3. is not a complete model of this geometry).

Diagram 3

A more complete model of this geometry is demonstrated in our last diagram, artfully embellished by the famous Dutch artist, M.C. Escher. The lines in this geometry are the arcs of circles visible there and many others, including the traditional line segments through the center of the space.

— Ellen H. Fenwick

Note: You might also enjoy Deriving Basic (Circular) Trigonometric Functions

← Back to Math-Logic-Design
← Home