Consider a simple equilateral triangle (a triangle that has 3 equal sides and 3 equal angles). Most high-school students know the three angles of such a triangle are 60 degrees (60°) each, for a total of 180°. But degrees is not the only unit used to quantify an angle. Alternately radians can be used. What are radians? Are they just another number? Where do they come from?
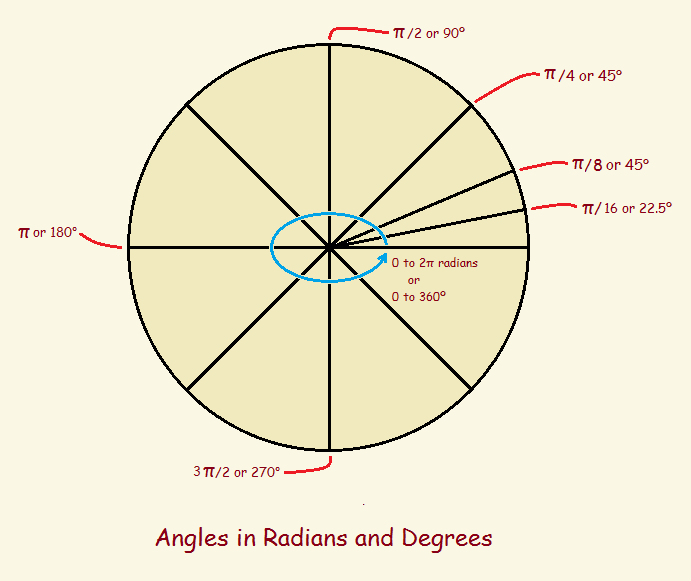
Degrees
Before we get into radians, however, let’s consider where degrees came from, and why it may not be the best choice for the measurement of an angle. If you are facing north and turn to the east, you have turned 90 degrees. Now turn south and you’ve turned another 90 degrees. Turn west, another 90 degrees. Continue the turn so you once again face north, and you’ve rotated through an angle of 360 degrees.
In rotating through a circle, you have turned 360 degrees. But why should a circle consist of 360 degrees? That number was chosen on purpose, though the reason for it is no longer certain. It may have to do with the early lunar calendar, which was 360 days in length. The earth experiences one rotation a year, or about 1 degree per day. There are other theories on the matter.
Adopting the degree as the standard works OK for some applications. Still, it is somewhat arbitrary. Mathematicians devised a better choice. They came up with the radian.
Radians
First, to see what a radian is, since “a picture is worth 1,000 words,” notice the animated gif visual by Lucas V. Barbosa, below.
As helpful as this is, it doesn’t provide the details of how the radian was conceived or why it is useful. A superb introductory explanation lasting ten minutes fifty seconds is seen in this video produced by Khan Academy.
Choose a Better “Language”
There’s more. In measuring an angle by the degree method, the number, such as 30 or 45 requires the descriptor degrees. An angle is 30 degrees or 45 degrees (30° or 45°). But since the definition of a radian divides a length by a length, there is no descriptor requirement. The equivalent of 30° and 45° is π/6 and π/4, respectively. These latter values are pure numbers. The abbreviation rad (radians) is sometimes used, but only to remind the reader what is being discussed.
Just as multiple languages can be used to convey the same basic message, but one can express it more beautifully, more simply, or more economically (fewer words), so the differing measure of angles conveys the same information. Radians is a superior language to degrees for the mathematician, especially for trigonometry and calculus. Some examples of this are demonstrated at the reference sites, below.
Note: You might also enjoy Simplifying Mathematics: Introducing Vectors and Vector Addition
References:
← Back to Math-Logic-Design
← Home
