 I had some excellent high school mathematics instructors. They both loved their field and took an interest in their students. Since high school, I have had a deep interest in collapsing 3D mathematical equations to derive equations for 2D mathematical objects or modifying 2D objects into other 2D, or 2D objects into 1D.
I had some excellent high school mathematics instructors. They both loved their field and took an interest in their students. Since high school, I have had a deep interest in collapsing 3D mathematical equations to derive equations for 2D mathematical objects or modifying 2D objects into other 2D, or 2D objects into 1D.
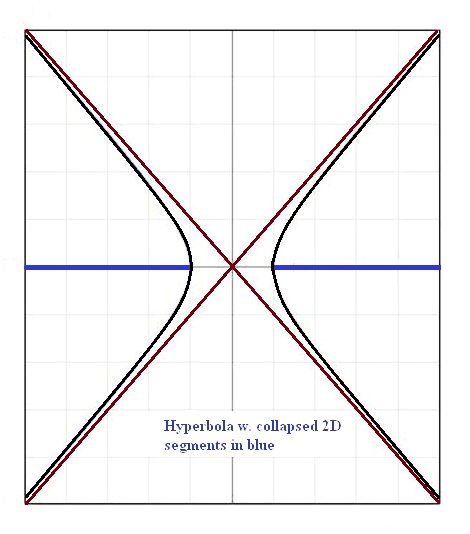
A 3D sphere becomes a 2D circle. A 2D parabola becomes a 1D line. The 2D hyperbola shown, if collapsed along the x-axis, becomes two 1D line segments stretching at one end to infinity. The same hyperbola collapsed along the y-axis becomes a complete line. A 2D circle becomes a single 1D line segment of a length equal to the diameter.
An Example of Collapsing 3D into 2D
What can be obtained by collapsing 3D math objects of a more complex sort? Let’s consider collapsing a simple cone aligned along the y-axis and centered at the origin, described by the equation, x2 + z2 = ky2. Such a cone can be collapsed because all the terms containing one variable can be isolated from all terms that contain the other variables.
If x = 0, for instance, the equation becomes z2 = ky2. This graphs as two intersecting lines. That makes sense, since if you could cast a shadow of a solid 3D cone, you would basically see two open-ended triangles. However those triangles are actually hollow, so you could really only expect to see the outline.
If, instead, z = 0, then x2 = ky2. The same situation applies here as in the first case, except the lines are facing in directions perpendicular to the others.
If y = 0 then z2 = ‒x2. This is only one point, since the square root of a negative number in the real world is imaginary (see however, this article on imaginary numbers. That point coincides with the origin.
← Back to Math-Logic-Design
← Home
